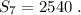q = 0,5
b3 = 320
s7 - ?
якщо q≠1, Sn = b1(q^n -1)/(q-1)
s7 = b1(q^7 -1)/(q-1)
b3 = b1 * q^2 ---> b1 = b3/q^2 = 320/0,5^2 = 1280
s7 = 1280(0,5^7 -1)/(0,5-1) = 2540
ВІДПОВІДЬ: 2540
Теорема 1 (теорема Фалеса). Параллельные прямые высекают на пересекающих их прямых пропорциональные отрезки (рис. 1).
Определение 1. Два треугольника (рис. 2) называются подобными, если соответствующие стороны у них пропорциональны.
Теорема 2 (первый признак подобия). Если угол первого треугольника равен углу второго треугольника, а прилежащие к этим углам стороны треугольников пропорциональны, то такие треугольники подобны (см. рис. 2).
Теорема 3 (второй признак подобия). Если два угла одного треугольника равны соответственно двум углам другого треугольника, то такие треугольники подобны (рис. 3).
Теорема 4 (теорема Менелая). Если некоторая прямая пересекает стороны AB и BC треугольника ABC в точках X и Y соответственно, а продолжение стороны AC — в точке Z (рис. 4), то
Теорема 5. Пусть в остроугольном треугольнике ABC проведены высоты AA1 и CC1 (рис. 5). Тогда треугольники A1BC1 и ABC подобны, причем коэффициент подобия равен cos ∠B.
Лемма 1. Если стороны AC и DF треугольников ABC и DEF лежат на одной прямой или на параллельных прямых (рис. 6), то
Лемма 2. Если два треугольника имеют общую сторону AC (рис. 7), то
Лемма 3. Если треугольники ABC и AB1C1 имеют общий угол A, то
Лемма 4. Площади подобных треугольников относятся как квадрат коэффициента подобия.
ответ: