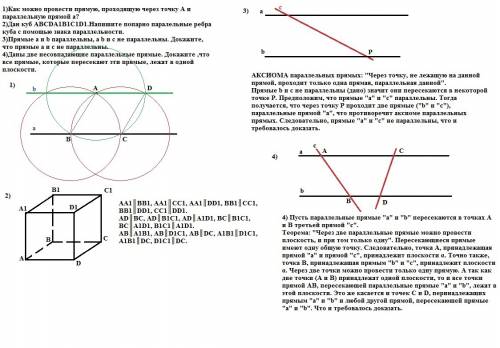
Автор поделился оригинальным текстом задания:
точка А лежит в плоскости, точка c на растоянии 3,5м от этой плоскости .Найдите расстояние от плоскости до точки М, делящей отрезок АС в отношении АМ:МС=2:5
Нарисуем перпендикуляр из C на плоскость. В месте пересечения с плоскостью поставим точку О.
CO по условию задачи = 3.5 метра
Затем отметим точку М на отрезке AC и проведем перпендикляр r плоскости MK
Треугольник AKM подобен OAC так как два их угла равны между собой(один общий, второй 90 градусов).
AM = 2/7 CA. (по условию) значит MK = 2/7 * CO = 2/7*3.5 = 1м
Это и есть ответ: 1м

ДВ=16см
обозначим вершины треугольника А В С, а точку от которой проведён перпендикуляр Д к вершине В: перпендикуляр ДВ. Наклонная, проведённая к стороне АС пересекает её в точке Н. Нам нужно найти перпендикуляр ДВ. Для этого проведём от вершины В высоту ВН к стороне АС=14см. Высота ВН является проекцией наклонной ДН. Найдём высоту через площадь ∆АВС по формуле Герона:
где р- полупериметр, а ab, bc, ac - стороны ∆АВС.
Найдём периметр треугольника:
Р=13+14+15=42; Р/2=42÷2=21см
Итак: S=84см².
Теперь найдём ВН, зная площадь и сторону треугольника, используя формулу площади:
S=1/2×АС×ВН
ВН=S÷1/2÷AC=84×2÷14=168÷14=12см
Наклонная ДН, её проекция на площадь треугольника ВН и перпендикуляр ДВ образуют прямоугольный треугольник с катетами
ВН и ДВ и гипотенузой ДН. Найдём искомый катет, он же перпендикуляр ДВ по теореме Пифагора:
ДВ²=ДН²– ВН²=20²-12²=400-144=256; ДВ=√256=16см