O - центр вписанной окружности.
Радиус в точку касания перпендикулярен касательной.
OMA=ONA=90 => A+O=180 => A+∪MN=180
Аналогично С+∪PQ=180
Сумма противоположных углов вписанного четырехугольника 180.
A+C=180 => ∪MN+∪PQ=180 => MPN+PNQ=90 => T=90

Дано: А(-3; 9), В(-4; -8), С(6; 0)
Найти:
а)координаты вектора АС;
б)длину вектора ВС;
в)координаты середины отрезка АВ:
г)периметр треугольника АВС;
д)длину медианы СМ.
a) AC = {Cx - Ax ; Cy - Ay}
AC = {6 - (-3) ; 0 - 9}
AC ={9 ; -9}
б) BC = {Cx - Bx ; Cy - By}
BC = {6 - (-4); 0 - (-8)}
BC = {10 ; 8}
|BC| =  =
= 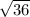 = 6
= 6
в) Пусть это будет точка M, тогда её координаты будут равны
M((Ax + Bx)/2 ; (Ay + By)/2)
M((-3 + -4)/2 ; (9 + 8)/2)
M(-3,5 ; 8,5)
г) Посчитаем длину каждой стороны треугольника
AB = 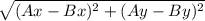 =
= 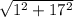 =
= 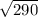
AC = 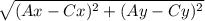 =
= 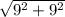 =
= 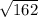
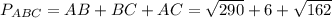
д) СМ = 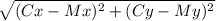 =
= 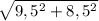 =
= 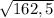
![\sqrt[n]{x}](/tpl/images/0258/0436/b773b.png)
Дуги MQN и QMP, если подумать равны 540 градусам, тк их градусная мера равна 2 кругам, из которых вырезали 180 градусов (как раз сумму углов MBN и QDP)
Объяснение: