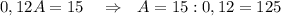Для решения этой задачи, мы можем воспользоваться свойствами касательных к окружностям.
Известно, что касательная, проведенная к окружности, перпендикулярна радиусу, проведенному к точке касания.
Поэтому, в треугольнике ABC, отрезок AC является радиусом окружности AK, а отрезок BC - радиусом окружности B.
Теперь, для решения задачи, мы можем применить теорему Пифагора.
Так как AB = 3 и AC = 12, мы можем найти отрезок BC, используя теорему Пифагора:
BC^2 = AC^2 - AB^2
BC^2 = 12^2 - 3^2
BC^2 = 144 - 9
BC^2 = 135
BC = √135
BC = 3√15
Также, мы знаем, что отрезок BC является радиусом окружности B, а отрезок AC - радиусом окружности AK.
Тогда, AK = AC - BC
AK = 12 - 3√15
ответ: неизвестное число = 125 .
Обозначим неизвестное число через А.
Тогда 60% от числа А равны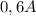
.
Найдём 20% от числа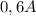
. Это будет 
.
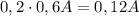По условию