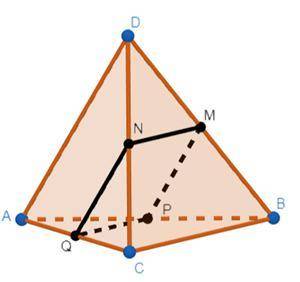
Стороны искомого четырехугольника являются средними линиями соответвенно QN- ΔCAD; NM -ΔCBD; MP- ΔABD; QP - ΔABC, а как известно, средняя линия параллельна основанию треугольника и равны половине соответствующего основания.
Поэтому периметр четырехугольника MNQP равен P=QN+NM+MP+QP =0.5*(2АD +2ВС)=АD +ВС=14+16=30/см/
1 у них один угол напротив лежащий и две стороны одинаковые , всё они подобны по одному углу и двум сторонам
3 там не всё видно но я предпологаю что там ещё одни углы равны поэтому треугольники равны по стороне и двум углам т к снизу два угла равны одни из сторон равны и тот угл
4 одни из сторон равны и равны одни углы и т к это параллелограмм то у них противоположные углы равны поэтому эти треугольники равны по одной стороне и двум углам
11 там вообще легко даётся что две стороны равны осталось найти угл между ними и их можно найти 180градусов - те углы которые на плоскости и всё и треугольники равны по двум сторонам и углу между ними
ответ: Р=30 см .
Так как M , N , P , Q - середины отрезков DB , DC , AC , AB , то отрезки MN , NQ , QP , MP - средние линии треугольников CDB , ADC , ADB , ABC соответственно.
Средняя линия треугольника параллельна соответствующей стороне треугольника и равна её половине .
MN║BC , MN=16:2=8 , NQ║AD , NQ=14:2=7 ,
MP║AD , MP=14:2=7 , PQ║BC , PQ=16:2=8
P(MNQP)=8+7+7+8=16+14=30 (cм)