
Дано: прямоугольный Δ АКО с прямым углом К. АК=2√3;
∠КАО=30°; ОК и АО - ?
Катет, лежащий против ∠30°=1/2 гипотенузы.
ОК=х; ОА=2х
По т.Пифагора ОА²=АК²+ОК²
(2х)²=х²+(2√3)²
3х²=4*3
х²=4
х=2 см - ОК
2х=4 см - АО
ответ: катет КО=2 см; гипотенуза ОА=4 см.
Дано:
P-12 см
Сторона -5см
Найти:
Основание-?
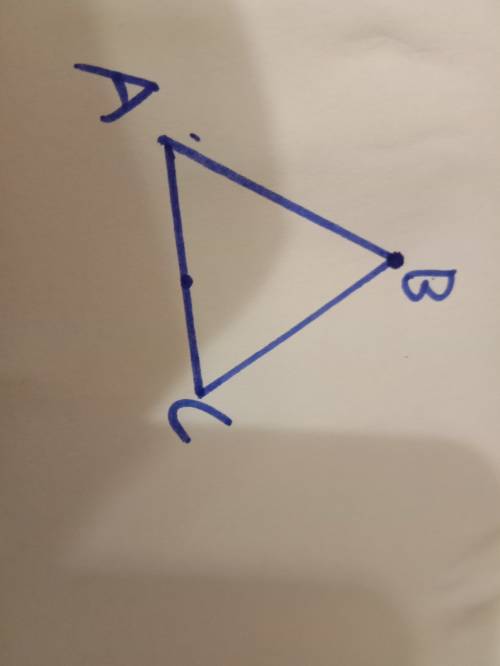
Периметр -это сумма длин всех сторон треугольника. Допустим, что у нас треугольник ABC. (смотри картинку) Так как у треугольника Два основания одинаковы, значит, что вторая сторона тоже будет равна 5 см. Чтобы найти боковую сторону надо сложить два основания и из периметра вычесть сумму основания. Вот действия:
1) 5+5=10 (см) - две основные стороны
2) 12-10=2 (см) -это боковая сторона.
ответ: боковая сторона =2 см.
Чтобы лучше запомнил(а) я напишу, как найти боковую сторону у треугольника ABC.
AB и BC - основания.
AC-боковая.
Так как AB =5см , то и BC =5 см.
Периметр - 12 см. Нужно найти AC.
1) AB+BC=5+5=10 (см)- основание AB и BC.
2) P-(AB+BC)=12-10=2 (см) - боковая сторона- AC.
ответ: боковая сторона AC =2 см.
Надеюсь
Дано:
P-12 см
Сторона -5см
Найти:
Основание-?
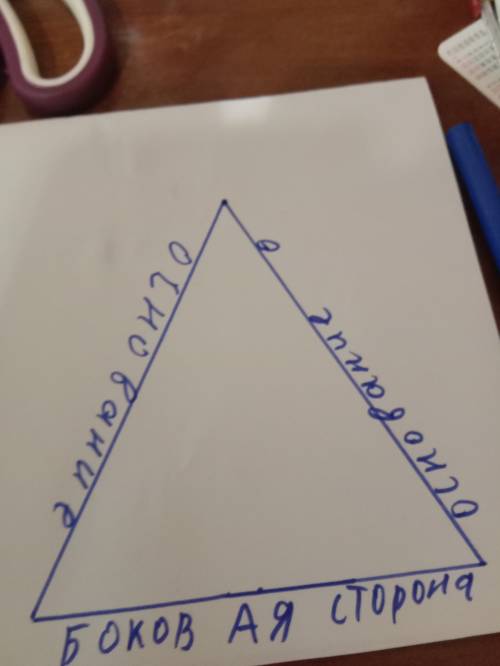
Периметр -это сумма длин всех сторон треугольника. Допустим, что у нас треугольник ABC. (смотри картинку) Так как у треугольника Два основания одинаковы, значит, что вторая сторона тоже будет равна 5 см. Чтобы найти боковую сторону надо сложить два основания и из периметра вычесть сумму основания. Вот действия:
1) 5+5=10 (см) - две основные стороны
2) 12-10=2 (см) -это боковая сторона.
ответ: боковая сторона =2 см.
Чтобы лучше запомнил(а) я напишу, как найти боковую сторону у треугольника ABC.
AB и BC - основания.
AC-боковая.
Так как AB =5см , то и BC =5 см.
Периметр - 12 см. Нужно найти AC.
1) AB+BC=5+5=10 (см)- основание AB и BC.
2) P-(AB+BC)=12-10=2 (см) - боковая сторона- AC.
ответ: боковая сторона AC =2 см.
Надеюсь


AO = 4
KO = 2
Объяснение:
cos30°=AK/AO
==> AO = 4
Из теоремы Пифагора АК² + KO² = AO²
==> KO =2