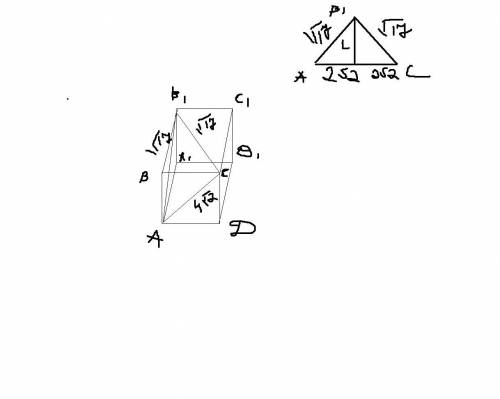
в основании правильной четырехугольной призмы лежит квадрат. и она прямая.
значит все боковые грани равны, отсюда S/4 = s1 (s1 - площадь одной грани)
16/4 = 4 = s1
зная диагональ основания найдем ее сторону так как a√2 = d
4√2 = a√2, а = 4
s1 грани равно = а*b = (а сторона основания, b высота призмы)
4 = 4*b, b = 1
найдем диагональ грани по теореме пифагора: х" = 16+1, х = √17
на рисунке видно сечение: АВ1С
из этого треугольника найдем ее высоту L: L" = 17-8 =9
L = √9 = 3
s = h*a*1/2 = 3*4√2*1/2 = 6√2
S(ACN) = 96
Объяснение:
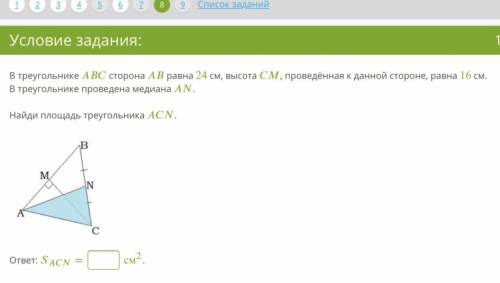
Площадь треугольника находится по формуле: S = a*h/2 , сторона умноженная на опущенную на неё высоту и делённая на два.
Вспомним свойство Медианы, Медиана делит Сторону и Площадь пополам, это значит что S(ACN) = S(ABC)/2
S(ABC) = AB*CM/2 находим общую площадь
S(ABC) = 24*16/2 = 24*8 = 192
S(ACN) = 192/2 = 96 делим на два и получаем площадь закрашенной части, поскольку она равна половине всей площади, по свойству медианы.