Відповідь:
Пояснення:
розв'язання завдання додаю

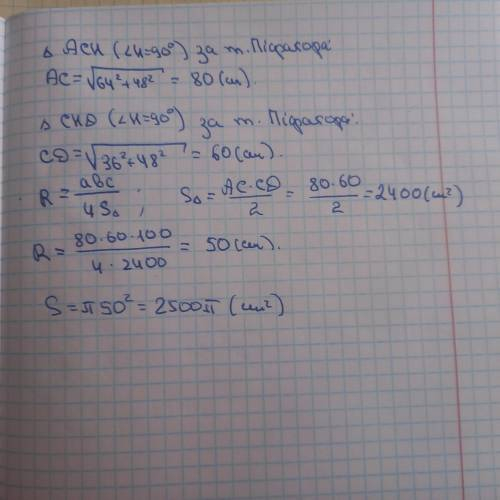
Задача
Дано:
периметр равностороннего треугольника 18 см
периметр равнобедренного треугольника 20 см
Сторона равностороннего треугольника является основанием равнобедренного треугольника
Найти: стороны равнобедренного треугольника
Решение
1) 18:3=6 (см) - сторона равностороннего треугольника;
2) пусть боковые стороны равнобедренного треугольника равны х см, тогда
х +х + 6 = 20
2х=20-6
2х=14
х=7 (см) - боковые стороны равнобедренного треугольника;
ответ: стороны равнобедренного треугольника равны 6 см, 7 см и 7 см.
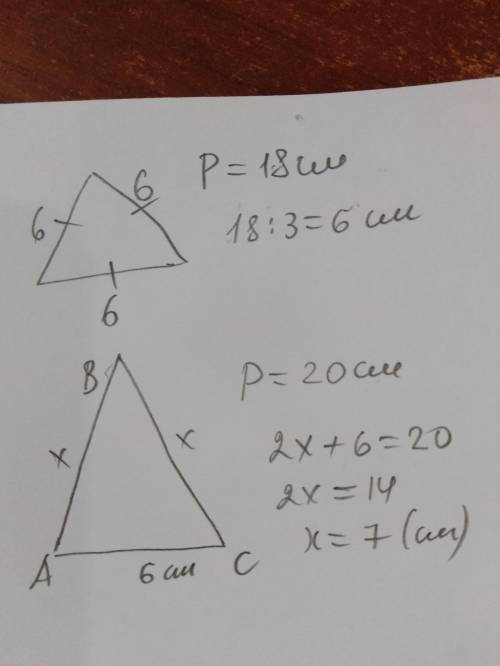
Сколько песчинок на Земле или даже в пустыне, подсчитать сложно. Но зато можно довольно легко установить приблизительное число их в одном кубическом метре песка. Подсчитав, мы обнаружим, что в таком объеме количество песчинок определяется астрономическими цифрами в 1,5— 2 миллиарда штук.
Таким образом, сравнение Шахерезады было по меньшей мере неудачным, так как если бы сказочным царям понадобилось столько солдат, сколько содержится зерен только в одном кубическом метре песка, то для этого пришлось бы призвать под ружье все мужское население земного шара. Да и этого было бы недостаточно.
Геологи установили, что их возникновение имеет длинную и сложную историю. Прародителями песка являются массивные породы: гранит, гнейс, песчаник. Мастерской, в которой происходит процесс превращения этих пород в песчаные скопления, является сама природа.
Объяснение:
Можемо використати властивість прямокутного трикутника, де одна сторона є діаметром кола, описаного навколо цього трикутника. У нашому випадку, діагональ трапеції буде діаметром кола. Застосуємо теорему Піфагора для знаходження радіуса:
Радіус^2 = (половина основи)^2 + висота^2
В нашому випадку, половина основи дорівнює 28/2 = 14 см, а висота - 100 см.
Радіус^2 = 14^2 + 100^2
Радіус^2 = 196 + 10000
Радіус^2 = 10196
Радіус = √10196 ≈ 100.98 см
Отже, радіус кола, описаного навколо трапеції, приблизно дорівнює 100.98 см. Для знаходження площі кола використовуємо формулу:
Площа = π * радіус^2
Площа = 3.14 * 100.98^2 ≈ 31827.7 см^2
Отримана площа кола, описаного навколо трапеції, становить приблизно 31827.7 см^2.