Обозначим начало наклонной А, конец наклонной В ( точка пересечения с плоскостью α).
Опустим из А перпендикуляр на плоскость α.
ВС- проекция наклонной а.
АС⊥ВС.
Угол АВС=45°
Прямую b обозначим ВК; угол АВК=60°
Рассмотрим треугольник АВС.
Так как угол АВС=45°, то угол ВАС=45°,
треугольник АВС прямоугольный равнобедренный.
АС=ВС=а*sin(45°)=(a√2):2.
Треугольник АВК прямоугольный.
ВК=а*cos(60°)=а:2
Треугольник ВКС - прямоугольный с гипотенузой ВС
cos ∠ KBC=BК:ВС=(а:2):(a√2):2=1:√2. Умножив числитель и знаменатель на √2, получим
cos ∠ KBC=√2):2. Это косинус 45°
а) Диагонали трапеции, пересекают среднюю линию, делят её на три равные части. Примем их по 1.
Левая и правая части средней линии равны половине верхнего основания., Оно равно 2.
2 правые или левые 2 части равны половине нижнего основания. Оно равно 4.
ответ: отношение равно 2:4 или 1:2.
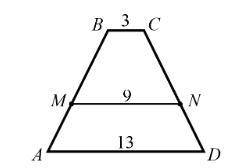
б) Отрезок MN параллелен основаниям трапеции ABCD (рис.), BC = 3, AD = 13, MN = 9. Найдите в каком отношении прямая MN делит боковые стороны.
Из точки С проведём отрезок параллельно АВ. получим 2 подобных треугольника с основаниями 9 - 3 = 6 и 13 - 3 = 10.
Боковые стороны в этом же соотношении: 6:10 = 3:5.
ответ: длины боковых сторон трапеции относятся 3:(5 - 3) = 3:2.
в) Найдите высоту равнобокой трапеции, диагональ которой равна d, а средняя линия равна m.
Проекция диагонали на основание равна ((а - b)/2) + b = ((a + b)/2) = m.
ответ: h = √(d² - m²).