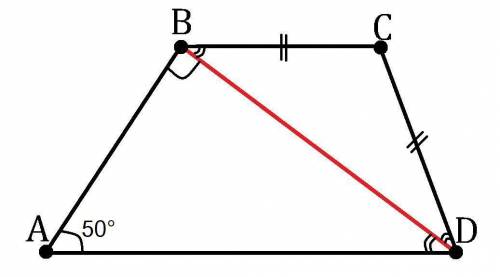
Дано: BC║AD; BD⊥AB; ∠BAD=50°; BC=DC.
Найти: ∠ABC, ∠BCD и ∠CDA.
∠BAD+∠ADB+∠DBA = 180° как сумма углов ΔBAD.
∠ADB = 180°-∠DBA-∠BAD = 180°-90°-50° = 40°
∠ADB = ∠DBC как накрест лежащие углы при параллельных прямых BC, AD и секущей DB.
∠DBC = ∠ADB = 40°.
ΔBCD - равнобедренный (по условию BC=DC), поэтому углы при его основании равны (∠DBC=∠BDC).
∠BDC = ∠DBC = 40°.
∠BCD = 180°-∠BDC-∠DBC = 180°-40°-40° = 100° т.к. сумма углов в треугольнике равна 180°.
∠ABC = ∠DBA+∠DBC = 90°+40° = 130°.
∠CDA = ∠ADB+∠BDC = 40°+40° = 80°.
ответ: 130°, 100° и 80°.
1) Диагонали параллелограмма равны. НЕВЕРНО
Диагонали равны только у разновидностей параллелограмма : у прямоугольника и квадрата.
2) Катет прямоугольного треугольника, лежащий против угла 30°, равен половине гипотенузы. ВЕРНО
3) В прямоугольной трапеции ровно один прямой угол. НЕВЕРНО
Боковая сторона, которая образует прямой угол с одним основанием трапеции, является перпендикуляром к двум параллельным основаниям, значит, она образует прямой угол со вторым основанием тоже. Всего в прямоугольной трапеции 2 прямых угла. Если в трапеции будет 4 прямых угла, то это будет прямоугольник.
4) Сумма углов четырёхугольника равна 360°. ВЕРНО
тогда,
тогда,
тогда,
Так что любая сторона больше разности двух его сторон. Что и требовалось доказать.