S1 = S2 = 2/3 ед². S3 = 1/3 ед². S4 = 4/3 ед² = 1 1/3ед².
Объяснение:
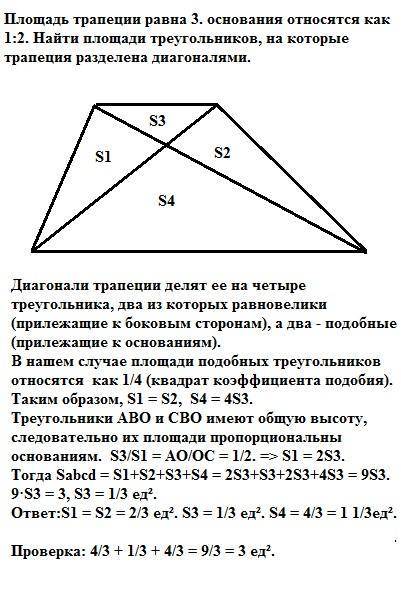
Диагонали трапеции делят ее на четыре треугольника, два из которых равновелики (прилежащие к боковым сторонам), а два - подобные (прилежащие к основаниям).
В нашем случае площади подобных треугольников относятся как 1/4 (квадрат коэффициента подобия). Таким образом, S1 = S2, S4 = 4S3.
Треугольники АВО и СВО имеют общую высоту, следовательно их площади пропорциональны основаниям. S3/S1 = AO/OC = 1/2. =>
S1 = 2S3.
Тогда Sabcd = S1+S2+S3+S4 = 2S3+S3+2S3+4S3 = 9S3.
9·S3 = 3, S3 = 1/3 ед².
ответ:S1 = S2 = 2/3 ед². S3 = 1/3 ед². S4 = 4/3 = 1 1/3ед².
Проверка: 4/3 + 1/3 + 4/3 = 9/3 = 3 ед².
V=312√3π(см³)
Объяснение:
осевым сечением цилиндра является прямоугольник. Обозначим его вершины А В С Д ч диагоналями АС и ВД, точку их пересечения К, а высоту ОО1. Объем цилиндра вычисляется по формуле: V=Sосн×ОО1, где основанием является окружность. Диагонали сечения пересекаясь делятся пополам поэтому АК=КС=ВК=ВД=10÷2=5см
Рассмотрим полученный ∆АКД. Он равнобедренный и <А=<Д=(180–60)÷2=120÷2=60°
Итак: ∆АКД- равносторонний, поскольку все его углы равны, и каждый составляет 60°, поэтому АК=КД=АД=5см.
Вычислим площадь сечения АВСД по формуле:
S=сеч½×AC²×sin60°=½×10²×√3/2=½×100×√3/2=
=25√3см²
Sсеч=25√3см²
Зная площадь сечения найдём высоту ОО1:
ОО1=Sсеч÷АД=25√3÷5=5√3см; ОО1=5√3см
Радиус АО1=О1Д=АД÷2=5÷2=2,5 см
Sосн=πr²=π×(2,5)²=6,25π
Теперь найдём объем цилиндра зная его площадь основания и высоту:
V=Sосн×ОО1=6,25π×5√3=312√3π(см³)