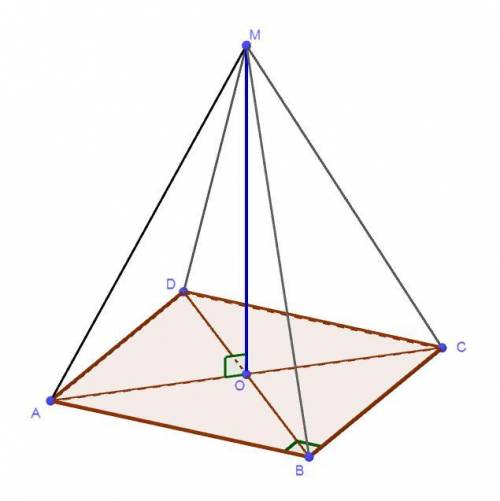
Точка пересечения диагоналей квадрата является центром квадрата. Т.к. из него проведена перпендикулярная прямая, значит расстояние от т. О до вершин квадрата будет одинаковое. Следовательно, нам нужно найти одно такое расстояние, чтобы знать все.
Стороны квадрата (а) равны. Диагонали у квадрата равные (d), и точк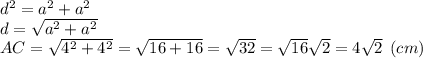
а пересечения делит их пополам.
Р-м ΔAOM:
∠O = 90°, AO — половина диагонали, OM — перпендикуляр к плоскости квадрата. АМ — наклонная.
AO = d/2
Ищем, чему равна диагональ квадрата:
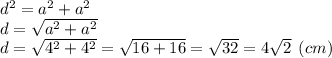
AO = (4√2)/2 = 2√2 см
Теперь можем найти длину отрезка AM
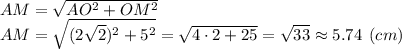
ответ: Расстояние равно √33 см, или приблизительно 5,74 см.
Объяснение:
Дано: ABCD-равнобедренная трапеция.
ВЕ и СF-высоты.
(а) Рассмотрим ΔАВЕ и ΔDCF.
∠А=∠Д и АВ=СД т. к. трапеция равнобедренная, ∠АЕВ=∠DFC=90°, а ∠А=∠Д поэтому ∠АВЕ=∠FCD ⇒ ΔАВЕ=ΔDCF.
(б) ∠А=∠Д, ∠Е=∠F, ∠В=∠С.
(с) Вид может быть разным, смотря как ВЫ начертите трапецию. Если у вас трапеция будет длиноватая, то это прямоугольник, если же получится так, что ЕВ=ВС=FC=EF, это квадрат.
(д) У нас ∠АВЕ=∠FCD, ВЕ и СF-высоты⇒∠В=∠Е=∠С=∠F=90°, т. е. ∠В=∠С, поэтому ∠АВС=∠ДСВ.
(е) У равнобокой трапеции есть свойство, это свойство и будет ВЫВОДОМ.
Вывод:
Углы при каждом основании равнобедренной трапеции равны.
треугольник равнобедренный,а это значит,что две стороны его равны АВ=ВС. 12УМНОЖИТЬ НА 2 = 24. ПЕРИМЕТР 32 значит 32-24=8 высота в равнобедренном треугольнике является и гипотенузой и биссектрисой. АС/2=4. ПЛОХО ВИДНО.
УГОЛ ВСК= СУММЕ ДВУХ ВНУТРЕННИХ УГЛОВ ТРЕУГОЛЬНИКА