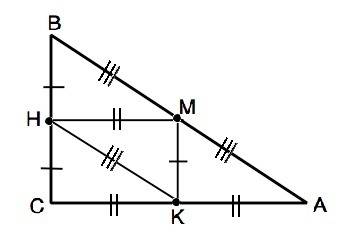
Средняя линия треугольника соединяет середины двух сторон треугольника, параллельна и равна половине третьей стороны. Средние линии делят исходный треугольника на 4 равных ( см. рисунок). Треугольник, образованный средними линиями треугольника, подобен исходному ( по равенству соответственных углов, образованных при пересечении параллельных средней линии и стороны треугольника секущей – стороной исходного треугольника). Коэффициент подобия k=1/2. Треугольник со сторонами 3,4, 5 - египетский, т.е. прямоугольный. Его площадь - половина произведения катетов. S=3•4:2=6 см²
Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Если исходный треугольник АВС, а середины его сторон К, М, Н, то Ѕ(КМН)=1/4•Ѕ(АВС)=1,5 см²
Каждый такой треугольник - грань развёртки тетраэдра. Площадь грани - 1,5 см²
↓↓↓↓↓↓↓↓↓↓↓↓
Объяснение:
R=3,94cm π=3,14
c=2*π*R , с=2*3,14*3,94=24,7432 см
R=10,6cm π=3,14
S=πR² ,S=3,14*10,6² =352,8104 см²