Сумма углов треугольника равна 180°
ABC' — треугольник. Проведем через вершину B прямую, параллельную прямой AC. Отметим на ней точку D так, чтобы точки A и D лежали по разные стороны прямой BC.Углы DBC и ACB равны как внутренние накрест лежащие, образованные секущей BC. Поэтому сумма углов треугольника при вершинах B и С равна углу ABD.Сумма всех трех углов треугольника равна сумме углов ABD и BAC. Так как эти углы внутренние односторонние для параллельных AC и BD при секущей AB, то их сумма равна 180°. Теорема доказана.
192
Объяснение:
Пусть трапеция АВСД ,высота ВН и СЕ.
Т.к трапеция равнобедренная , то АВ+СД=АД+ВС=32.
АД-ВС=18 ⇒ АН=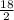
=9
ΔАВН, гипотенуза 5 частей, катет 4 части( египетский треугольник)⇒последний катет 3 части. Тогда на одну часть 9:3=3 см.
ВН=4*3=12 см
S=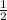
*h*(a+b) , S= 
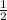*12*32=192