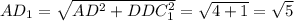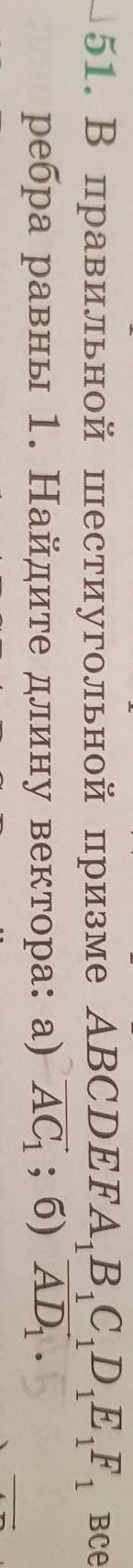
Возьми листок бумаги и нарисуй рисунок сначала!Как нарисовала читай дальше! :) Тут есть два варианта решения! Вот посмотри на строны AO,BO,CO! Они все радиусы, а значит равныРассматриваем треугольники AOB и AOC.Они равны по двум стронам и углом между ними(AO-общая; BO=OC(как радиусы), угол AOB = углу AOC( угол AO = 90 градусов по условию, а сам угол BOC = 180(развёрнутый).Соответственно угол AOC= угол BOC - угол AOB = 90 градусов!).Ну а если треугольники равны, то и все их элементы тоже равны, откуда следует, что AB=AC!
Второй вариант заключается в правиле перпендикуляра!Если одна сторона( в нашем случае AO) ,,падает,, на любую другую сторону под углом 90 градусов, а точки произвольные находятся на одинаковом расстоянии от места падения, то любая точка на этой падающей прямой равноотдалены от их концов( произвольных точек). В нашем случае это точки B и С! :)
Треугольник МКР, МТ=5, КТ=10, МК=15, КР=9, М=12
Периметр = 15+9+12=36, полупериметр=36/2=18
Площадь МКР= корень (18 х (18-15) х (18-9) х (18-12) = корень 2916=54
плошадь МКР = 1/2 х МК х КР х sin угла K
54 = 1/2 х 15 х 9 х sin угла K , sin угла K = 108/135=0,8
МР/ sin угла K = КР / sin угла М, 12 / 0,8 = 9 / sin угла М, sin угла М = 0,8 х 9/12=0,6
площадь треуг КТР = 1/2 х КТ х КР х sin угла K = 1/2 х 10 х 9 х 0,8 =36
площадь МТР = 1/2 х МТ х МР х sin угла М = 1/2 х 5 х 12 х 0,6 =18
Всего 36+18=54
AC₁=2
AD₁=√5
Объяснение:
1. Рассмотрим ΔАВС (см. рис. 1). Он равнобедренный с АВ=ВС=1 и ∠В=120° (как внутренний угол правильного шестиугольника). Опустим высоту ВО на АС. Получили два равных прямоугольных ΔАВО = ΔСВО с углами 60°, 30° и 90° (т.к. ВО в равнобедренном тр-ке есть биссектрисой).
По теореме Пифагора,
тогда АС=АО*2=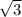
Рассмотрим ΔACC₁ (см. рис. 3). Он прямоугольный с двумя известными катетами
АС=√3, CC₁=1. Гипотенуза АС₁ является искомой величиной.
По теореме Пифагора: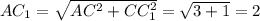
2. Рассмотрим ΔACD. Он прямоугольный с двумя известными катетами
АС=√3, CD=1 (см. рис. 2). Найдем гипотенузу АD.
Рассмотрим ΔADD₁ (см. рис. 4). Он прямоугольный с двумя известными катетами
АD=2, DD₁=1. Гипотенуза АD₁ является искомой величиной.
По теореме Пифагора: