Сумма двух сторон треугольника не может быть равна или меньше длины его третьей стороны.
Следовательно, третья сторона не может быть равна или больше суммы двух других, т.е. х ≨ 2,9
В то же время сумма третьей и одной из двух сторон не может быть меньше оставшейся стороны.
Пусть периметр треугольника
(0,8+2,1)+х=2,9+х
Тогда
0,8+х > 2,1
2,1+х > 2,9
До целого числа периметру треугольника недостает:
1).
0,1 м
Третья сторона не может быть такой длины.
Иначе сумма сторон 0,8+0,1=0,9, а оставшаяся сторона 2,1 больше, чем 0,9
2).
1,1 м
сумма сторон 0,8+1,1=1,9, а оставшаяся сторона 2,1 > 1,9
1,1- не подходит
3)
2,1
.. 0,8+2,1=2,9
Третья сторона этого треугольника может быть только 2,1 м.
Построение сечения: Назовем искомую плоскость MNK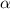
. Плоскости ABC и A1B1C1 параллельны и пересечены плоскостью 
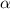, следовательно, линии пересечения параллельны. Значит, 
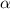пересекает А1В1С1 по прямой КF, параллельной MN. Значит, F - середина А1В1. Осталось соединить KF, FM, MN, NK. Искомое сечение - FKNM.
Доказательство: В треугольнике ABD MN-средняя линия, MN || BD. Т.к MN лежит в плоскости сечения MNK, а BD параллельна прямой MN, лежащей в плоскости сечения, ВD параллельна плоскости MNK, что и требовалось доказать.