Розв'язання: Проведемо медіану до основи BC у точку K, тоді CK = BK =
= BC : 2 = 10 : 2 = 5 см.Нехай медіани AK і BM - перетинаються в
точці O.За теоремою про медіану, медіани точкою перетину діляться у відношенні 2 : 1, рахуючи від вершини кута.Введемо коефіціент пропорційності y, тоді BO = 2y,MO = y, так як медіани AK і BM - перетинаються в точці O.
BM = BO + MO;
8 = 2y + y;
8 = 3y;
y = ;
BO = 2y = 2 * ; MO = y = ;
За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, тоді за теоремою Піфагора: ;
Введемо коефіціент пропорційності x, тоді OK = x, AO = 2x за теоремою про медіану, так як медіани AK і BM - перетинаються в точці O.
AK = OK + AO;
AK = x + 2x = 3x = 3*OK = ;
За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, тоді за теоремою Піфагора:
Рассмотрим параллелограмм АВСД (см. рисунок) стороны которого: АВ=32 см, ВС=40 см. Из угла АВС проведем перпендикуляр ВЕ и расстояние между вершинам тупых углов ВД Рассмотрим треугольник АВЕ: Угол АЕВ=90 градусов, Гипотенуза АВ=32 см, Катет АЕ=16 см (по условию задачи) По теореме Пифагора найдем второй катет (высоту): ВЕ= √(АВ^2-АЕ^2)= √(32^2-16^2)= √(1024-256)= √768 см. Теперь рассмотрим треугольник BДE: ДЕ=АД-АЕ=40-16=24 см. ВЕ=√768 см. Угол ВЕД=90 градусов По теореме Пифагора найдем ВД: ВД=√(ВЕ^2+ВД^2)= √((√768)^2+24^2))= √(768+576)= √1344=8√21 см или приблизительно 36,66 см. ответ: расстояние между вершинами тупых углов равно 8√21 см
AB = AC =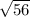
см
Объяснение:
Дано:
AC = AB, BC = 10 см, BM = 8 см, CM = MA
Знайти: AC,AB - ?
Розв'язання: Проведемо медіану до основи BC у точку K, тоді CK = BK =
= BC : 2 = 10 : 2 = 5 см.Нехай медіани AK і BM - перетинаються в
точці O.За теоремою про медіану, медіани точкою перетину діляться у відношенні 2 : 1, рахуючи від вершини кута.Введемо коефіціент пропорційності y, тоді BO = 2y,MO = y, так як медіани AK і BM - перетинаються в точці O.
BM = BO + MO;
8 = 2y + y;
8 = 3y;
y =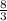
;
BO = 2y = 2 *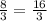
; MO = y = 
;
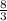За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, тоді за теоремою Піфагора: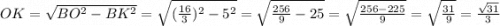
;
Введемо коефіціент пропорційності x, тоді OK = x, AO = 2x за теоремою про медіану, так як медіани AK і BM - перетинаються в точці O.
AK = OK + AO;
AK = x + 2x = 3x = 3*OK =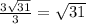
;
За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, тоді за теоремою Піфагора:
Так як AB = BC за умовою, то AB = AC =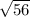
см.