Sastd = 67,5+15√3 см².
Объяснение:
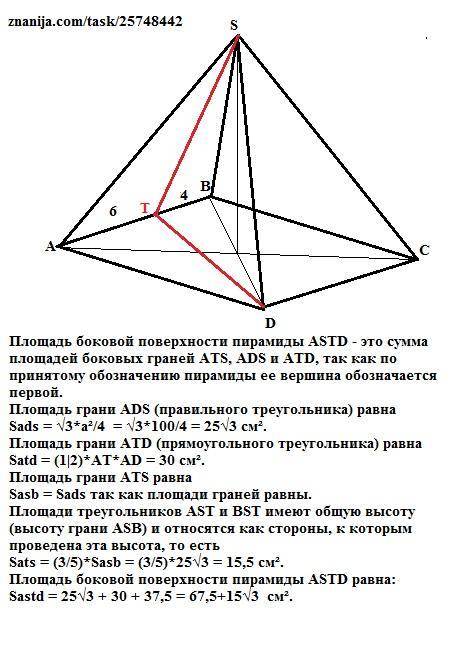
Площадь боковой поверхности пирамиды ASTD - это сумма площадей боковых граней ATS, ADS и ATD, так как по принятому обозначению пирамиды ее вершина обозначается первой.
Площадь грани ADS (правильного треугольника) равна
Sads = √3*а²/4 = √3*100/4 = 25√3 см².
Площадь грани ATD (прямоугольного треугольника) равна
Satd = (1|2)*AT*AD = 30 см².
Площадь грани ATS равна
Sasb = Sads = 25√3 см², так как площади граней равны.
Площади треугольников АST и BST имеют общую высоту (высоту грани ASB) и относятся как стороны, к которым проведена эта высота, то есть Sats/Sbts = 3/2. А так как Sasb = Sats+Sbts, то
Sats/Sasb = 3/5. тогда
Sats = (3/5)*Sasb = (3/5)*25√3 = 15,5 см².
Площадь боковой поверхности пирамиды ASTD равна:
Sastd = 25√3 + 30 + 37,5 = 67,5+15√3 см².
P.S. На всякий случай:
Площадь грани STD можем найти по Герону.
По теореме косинусов в треугольнике AST:
ST² = √(AT²+AS²-2*AT*AS*Cos60). (угол SAT = 60, так как грани - правильные треугольники). Тогда
ST = √(136-2*AT*AS*(1/2)) = √76.
DT = √(AT²+AD²) = √136.
SD = 10.
Полупериметр равен (10+√136+√76)/2 и по Герону:
Sstd = √((10+√136+√76)*(10+√76-√136)*(10+√136-√76)*(√136+√76-10))/4 или
Sstd = √((10+√76)²-136)*(136-(10-√76)²)/4 или
Sstd = √((20√76+40)*(20√76-40))/4 или
Sstd = √((30400-1600)/4 = √28800/4 = 120√2/4 =30√2.
1) Отношением двух отрезков называется частное их длин. Например,
АВ = 4 см, КР = 8 см
АВ : КР = 4 : 8 = 1 : 2
2) Пропорциональными называют пары отрезков, если равны их отношения. Например, если
АВ = 4 см, КР = 8 см, CD = 12 см, EF = 24 cм, то
АВ : CD = KP : EF = 1 : 3,
отрезки АВ и КР пропорциональны соответственно отрезкам CD и EF.
3) Подобными называются треугольники, если между их вершинами можно установить такое взаимно однозначное соответствие, что соответствующие углы равны и соответствующие стороны пропорциональны.
Например, треугольники АВС и МРК подобны, если
∠А = ∠М, ∠В = ∠Р, ∠С = ∠К и
АВ : МР = АС : МК = ВС : РК.
4) Число, равное отношению соответствующих сторон подобных треугольников, называется коэффициентом подобия. Обозначается k.
Коэффициент подобия показывает, чему равно отношение сторон подобных треугольников.
Чтобы его найти, надо найти отношение соответствующих сторон.
Например, если треугольники АВС и МРК подобны, то
АВ : МР = АС : МК = ВС : РК = k
5) Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Например, если треугольники АВС и МРК подобны, то
Sabc : Smkp = k²