

1) Рассм. Δ KMN; ∠KMN=90 - 60=30° по свойству острых углов прямоугольного Δ.
KN=(1/2)MN; MN=4.
MK=√(MN²-KN²)=√(16 - 4)=√12=2√3.
2) рассм. ΔРМК; МК=(1/2)МР
МР=2√3 * 2 = 4√3.
⇒ по Т.Пифагора КР=√(МР² - МК²)=√(16*3 - 4*3)=6
3) NP=KP - KN=6 - 2=4.
ответ: 4 линейных единицы.
Рисунок во вложении.
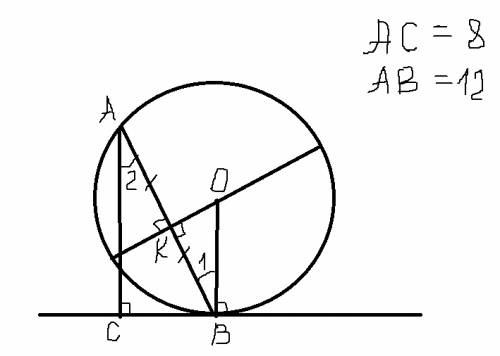
Назовем хорду АВ. Через точку В проведем касательную, из точки А проведем перепндикуляр АС к касательной-это и будет расстоянием от А до касательной. Получили прямоугольный треугольник АВС.
Теперь проведем диаметр окружности перпедикулярно хорде АВ. Он будет делить эту хорду пополам. Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею дуги пополам. Точку пересечения хорды и диаметра назовем К .
Проведем радиус ОВ. Так как ОВ перпендикулярен касательной и АС перпендикулярен касательной, то ОВ//АС. Углы 1 и 2 накрест лежащие, значит они равны.
Рассмотрим треугольники АВС и ВОК: они прямоугольные и имеют по равному острому углу, значит они подобны. Из подобия следует, что ОВ:АВ=АС:ВК => ОВ:12=6:8 => ОВ=9
ответ: 9см.
Объяснение:
Диагональ должна разделить прямоугольник на два прямоугольных треугольника. Сторонами (катетами) каждого тругольника будут являться 2 смежных стороны прямоугольника (7 м и 24 м). Диагональ будет являть гипотенузой этого прямоугольника. По теореме Пифагора найдем диагональ:
Диагональ должна разделить прямоугольник на два прямоугольных треугольника. Сторонами (катетами) каждого тругольника будут являться 2 смежных стороны прямоугольника (7 м и 24 м). Диагональ будет являть гипотенузой этого прямоугольника. По теореме Пифагора найдем диагональ:
х²=7²+24²=49+576=625
х=√625=25