Дан четырехугольник ABCD
AB=CD
BC=AD
угол A = 30⁰
E ∋ BC
угол CDE = 60⁰
Доказать. ABED - прямоугольная трапеция.
Доказательство.
Рассм. ABCD. угол A = 30⁰ ⇒ угол С = 30⁰
угол В = углу D = (360⁰ - 30⁰ - 30⁰)/2 = 300⁰/2 = 150⁰
угол ADE = угол ADC - угол CDE
т.к. угол ADC 150⁰, a по условию угол CDE = 60⁰, то угол AED = 150⁰ - 60⁰ = 90⁰
Опеределения:
- трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие не параллельны.
- трапеция, один из углов которой прямой, называется прямоугольной
Рассмотрим ABED - четырехугольник.
BE||AD,
AB не параллельно ED (т.к. ED перпендикуляр к AD)
угол EDA - 90⁰
След-но ABED - прямоугольная трапеция.
Объяснение:
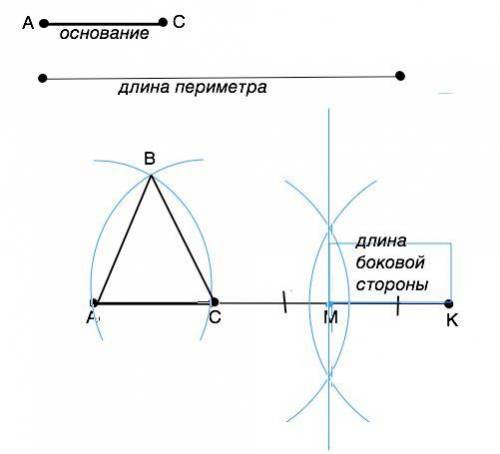
1) На произвольной прямой отложить отрезок, равный длине периметра. Обозначить его АК.
2) От т.А циркулем отметить на АК точку С, АС= длине данного основания.
3). Отрезок СК разделить на две равные части. Для этого из т.С и т.В провести две полуокружности до их пересечения по обе стороны от СК. Точки пересечения соединить прямой ( срединным перпендикуляром). Точку пересечения этой прямой и отрезка СК обозначить М. СМ=МК=длина боковой стороны треугольника.
4). Циркулем с раствором, равным МК, провести из точек А и С дуги до их пересечения. Точку пересечения обозначить В и соединить с т.А и т.С. Треугольник АВС - искомый.
продолжение луча – это такой луч, который имеет общее начало, но не совпадает с имеющимся лучом.