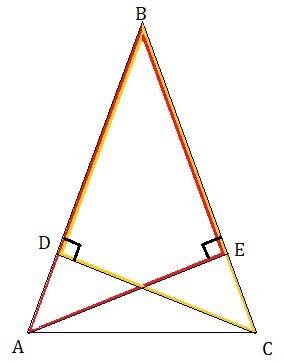
∠BEA = ∠BDC = 90° (так как AE и CD — высоты △ABC).
⟹ треугольники ABE и CBD прямоугольные.
Сумма острых углов прямоугольного треугольника равна 90°.
В треугольнике ABE ∠BAE = 90° — ∠B.
В треугольнике CBD ∠BCD = 90° — ∠B.
⟹ ∠BAE = ∠BCD, ∠B — общий,
BA = BC (как боковые стороны равнобедренного △ABC)
Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
⟹ треугольники ABE и CBD равны.
Из равенства треугольников следует равенство соответствующих сторон: AE = CD.
Что и требовалось доказать.
3м 5 дм 9 см - 395см
1м 4 дм 4см - 144см
359 - 144 -- 2 м 5дм 1 см