Поиск...
3
Избавься от ограничений
ПОПРОБУЙ ЗНАНИЯ ПЛЮС СЕГОДНЯ
Ruvioo
26.01.2015
Геометрия
5 - 9 классы
ответ дан • проверенный экспертом
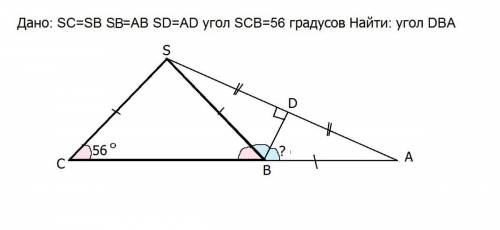
! Дано: SC=SB Sb=AB SD=AD угол SCB=56 градусов Найти: угол DBA
1
СМОТРЕТЬ ОТВЕТ
ответ, проверенный экспертом
3,0/5
19
Hrisula
главный мозг
7.7 тыс. ответов
83.3 млн пользователей, получивших
Треугольник SCB - равнобедренный по условию.
Углы при основании СВ равны. Угол SBC =SCB=56°
Угол SBA cмежный и равен 180°- 56°=124°
В треугольнике SBA по условию SB=BA, он тоже равнобедренный.
SD=DA, следовательно, ВD - медиана.
В равнобедренном треугольнике медиана является биссектрисой и высотой.
ВD - биссектриса,⇒ угол АBD - половина угла SBA и равен 124°:2=62°
Можно найти и угол DSB
Треугольник SDB- прямоугольный, т.к. ВD - высота.
Угол DSB равен 90°-62°=28°
Поиск...
3
Избавься от ограничений
ПОПРОБУЙ ЗНАНИЯ ПЛЮС СЕГОДНЯ
Ruvioo
26.01.2015
Геометрия
5 - 9 классы
ответ дан • проверенный экспертом
! Дано: SC=SB Sb=AB SD=AD угол SCB=56 градусов Найти: угол DBA
1
СМОТРЕТЬ ОТВЕТ
ответ, проверенный экспертом
3,0/5
19
Hrisula
главный мозг
7.7 тыс. ответов
83.3 млн пользователей, получивших
Треугольник SCB - равнобедренный по условию.
Углы при основании СВ равны. Угол SBC =SCB=56°
Угол SBA cмежный и равен 180°- 56°=124°
В треугольнике SBA по условию SB=BA, он тоже равнобедренный.
SD=DA, следовательно, ВD - медиана.
В равнобедренном треугольнике медиана является биссектрисой и высотой.
ВD - биссектриса,⇒ угол АBD - половина угла SBA и равен 124°:2=62°
Можно найти и угол DSB
Треугольник SDB- прямоугольный, т.к. ВD - высота.
Угол DSB равен 90°-62°=28°

В ∆ АВС высоты АА1 и СС1 со сторонами два прямоугольных треугольника АС1С и АА1С с общей гипотенузой АС.
Следовательно, вокруг них можно описать окружность с диаметром АС, на который опираются прямые углы АС1С и АА1С.
Вписанные углы А1АС и А1С1С опираются на одну дугу А1С. Вписанные углы, опирающиеся на одну дуга, равны. ⇒
∠СС1А1=∠САА1. Доказано.
Рассмотрим ∆ АОС1 и А1ОС.
Эти треугольники подобны по двум углам - прямому при С1 и А1 и вертикальному при точке пересечения высот О.
Из подобия следует пропорциональность сторон:
С1О:А1О=АО:СО,
откуда имеем пропорциональность тех же сторон в ∆ АОС и ∆ А1ОС1.
Вертикальные углы при вершине О этих треугольников равны.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Следовательно, углы СС1А1 и САА1 равны. Доказано.
Объяснение: