Дана правильная треугольная пирамида SABC с вершинойS,каждое ребро которой имеет длину,равную 2корень из 6. Точки K,M и N лежат на рёбрах SA,SB,SC соответственно так,что SK:SA=2:3,SM:MB=2:1, SC:SN=3:2. Найдите площадь сечения пирамиды плоскостью,проходящей через точки K,M,N
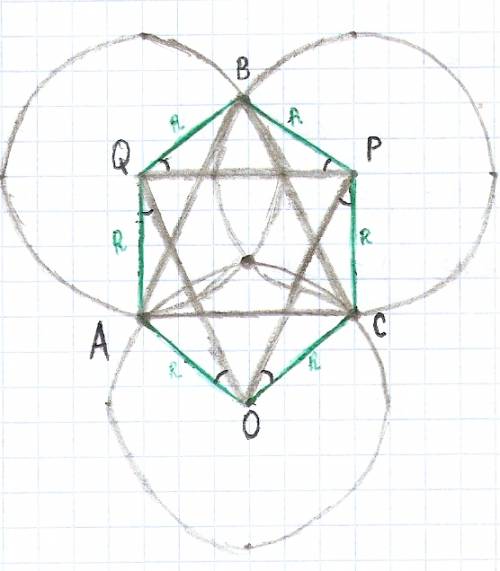
2.Рассмотрим 2 четырехугольника ОАQЕ и ОQРС -это ромбы, АО паралл QЕ, ОС паралл РЕ, следовательноугАОС=угQЕР, тогда из равенства треуг QЕР=треугАОС, следоват АС=QР
3. если рассмотреть два четырехугольника ОQВС и ОАВР, ОС парал ЕР и парал QВ, а таже они равны = R., значит ОQВС -параллелограм по (насколько помню) первому признаку тогда QO=BC, а так же они паралл. аналогично доказывается что ОАВР-параллелогр., а значит АВ=ОР, мы доказали, что в треуг ОРQ и АВС АС=QР, QO=BC, АВ=ОР, а раз три стороны соответственно равны, то треуг=.