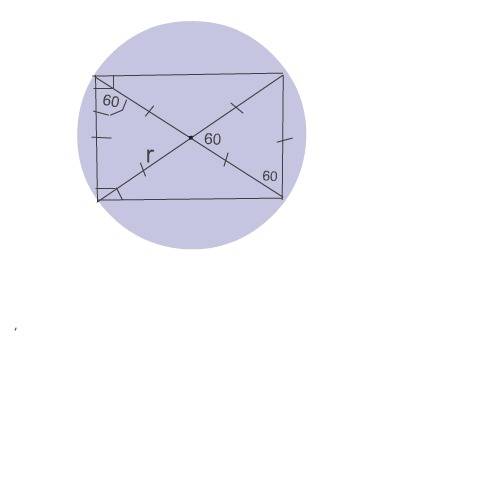
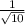Площадь круга, как Вы помните, находят по формуле
S=πr²
Радиус находим из остроугольных треугольников, образовавшимися диагоналями при меньшей стороне прямоугольника.
Эти треугольники - равносторонние, т.к. угол при пересечении диагоналей равен 60°, а сами диагонали делятся пополам и этим образуют равнобедренные треугольники, углы которых при основании, равном меньшей стороне вписанного прямоугольника, тоже равны 60°.⇒cледовательно, каждая половина диагонали равна меньшей стороне прямоугольника. А так как диагонали здесь являются диаметрами окружности, то радиус описанного круга тоже равен меньшей стороне прямоугольника.
r=10 см
S=πr²,
S=100 π см²
Найдите внешний угол при вершине С треугольника ABC, если известны координаты трех его вершин А(1; -2; -1), В(-1; 2; -1), С(-1; -2; -3)
Объяснение:
Найдем ∠АСВ . Тогда внешний угол α=180-∠АСВ.
cos(∠ACB)=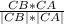 . Найдем координаты и длину векторов СВ и СА.
. Найдем координаты и длину векторов СВ и СА.
СВ(0;4;2) ,|CB|=√(0²+4²+2²)=√20 ;
СА(2;0;2) ,|CA|=√(2²+0²+2²)=√8.
cos(∠ACB)=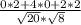 =
= 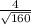 =
= 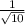 ⇒ ∠ACB=arccos
⇒ ∠ACB=arccos
α=180°-arccos