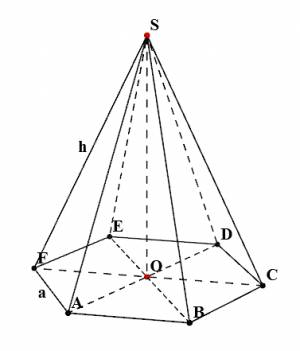
Высота SO=24, боковое ребро SА=25.
Треугольник AOS-прямоугольный, по теореме Пифагора найдем катет АО=SА в квадрате-SО в квадрате все под корнем=25 в квадрате-24 в квадрате все под корнем=7
По свойствам правильного шестиугольника, треугольник AOB является правильными треугольником. Отсюда следует, что АО=ОВ=АВ=7.
В правильной пирамиде все боковые грани равнобедренные треугольники. Треугольник АSВ-равнобедренный.
1. Найдем высоту проведенную к основанию АВ, она будет являться еще и медианой, и соответственно делить основание на 2 равных отрезка оавных 3,5. Высота образует прямоугольный треугольник с катетом 3,5 и гипотенузой 25. По теореме Пифагора найдем высоту=25 в квадрате-3,5 в квадрате все под корнем=612,75 под корнем
2. Площадь треугольника=0,5 основание*высоту или 0,5* сторону* высоту к стороне
Площадь=0,5*7*612,75 под корнем=3,5*(612,75 под корнем)
Тогда высота к боковой стороне=2*площадь/сторону=2*3,5*(612,75 под корнем)/25 =0,28 (612,75 под корнем)
Если, что решение я скопировал но мне можно потому, что там решал его Я (там такая же задача только под номером 4)
СFОЕ - квадрат( СФ = СЕ (касательные проведенные из пункта С) угол СFО = углу СЕО = 90 градусов( Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания))
СО - диогональ квадрата СFОЕ, найдем его стороны:
СЕ = ЕО( стороны квадрата) обозначим их через х
Найдем х по теореме Пифагора из тр. СОЕ
СО^2 = x^2 + x^2
8=2(x^2)
x^2=4
x=2
ОЕ = х = 2 см - это и есть наш радиус
Угол FОЕ = 90 градусов( СFОЕ - квадрат)
Угол FОЕ и FДЕ опираются на дугу FЕ, значит угол FДЕ = угол FОЕ/2 = 90 / 2=45 град. (вписаный в окружность угол равен половине центрального, который опирается на ту же дугу)
ответ: радиус 2 см; угол ФОЕ = 90 град.; угол ФДЕ = 45 град.
Попобуй в этот прилоюений оставит свой вопрос в течение 10 минут тебе минут ответит