трапеция авсд, высота вн пересекает диагональ ас в точке о, при этом во =10, он=8.; ав =вс=х по условию, значит треугольники аон и сов подобны по двум углам (так как угол вас =углу вса и углы при вершине о равны как вертикальные) из подобия треугольников следует пропорция вс/ан=во/он, т.е х/ан=10/8,значит ан= 4х/5 и всё нижнее основание ад= 4х/5+х+4х/5, т.е ад=13х/5. но из прямоугольного треугольника авн по теореме пифагора авв квадрате = ан в квадрате + вн в квадрате, т.е х в квадрате = (4х/5)в квадрате + 18 в квадрате. отсюда х=30. тогда верхнее основание вс=30,нижнее ад= 13х/5=78 и площадь трапеции равна полусумме оснований умножить на высоту, т.е (78+30)/2 и умножить на 18, получится 972.
ответ: 972
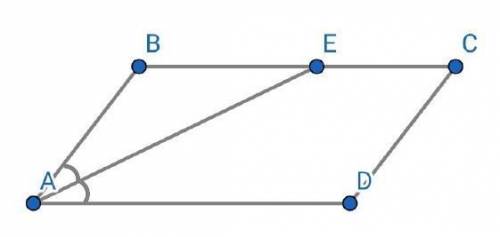
Четырёхугольник ABCD — параллелограмм.
Отрезок АЕ — биссектриса ∠А.
Е ∈ ВС.
ВЕ = 3*ЕС.
ВС = 12 [см].
Найти :Р(ABCD) = ?
Решение :Пусть ЕС = х, тогда, по условию задачи, ВЕ = 3х.
ВС = ВЕ + ЕС
12 [см] = 3х + х
4х = 12 [см]
х = 3 [см].
ВЕ = 3х = 3*3 [см] = 9 [см].
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.Следовательно, ∆АВЕ — равнобедренный (причём ВЕ = АВ = 9 [см]).
Периметр параллелограмма равен удвоенной сумме его смежных сторон.Следовательно, Р(ABCD) = 2*(AB + BC) = 2*(9 [см] + 12 [см) = 2*21 [см] = 42 [см].
ответ :42 [см].
Отношение длины стороны треугольника к синусу противолежащего угла равно двум радиусам описанной около треугольника окружности. Теорема косинусов: Квадрат стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними.
Объяснение: