Розв'язання:
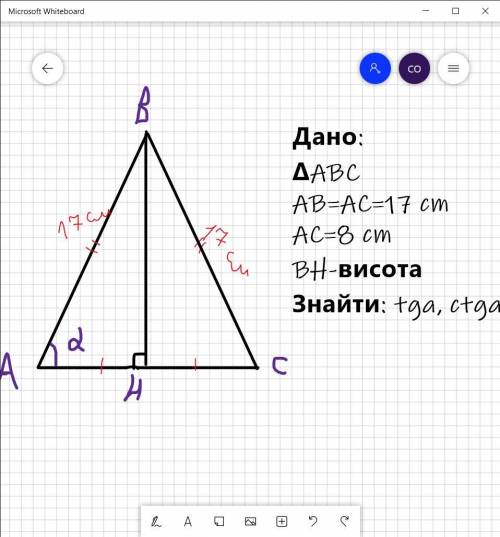
на фото малюнок і дано
Тангенс дорівнює відношенню протилежного катета до прилеглого
Отже, необхідно отримати прямокутний трикутник. Для цього проводимо висоту до основи. Оскільки трикутник рівнобедрений, то ця висота є одночасно і медіаною, отже АН=НС=8/2=4 см
Прилеглий катет (АН) тепер відомий, тож необхідно знайти протилежний за теоремою Піфагора
ВН²=АВ²-АН²=17²-4²=289-16=273
ВН=√273
tga=AH/BH=4/√273
ctga=1/tga=√273/4
Оскільки кути при основі рівнобедреного трикутника рівні, то і їхні тригонометричні значення рівні
Відповідь: tga=4/√273, ctga=√273/4
1.Первый признак (по двум катетам)
Если катеты одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.
2.Второй признак (по катету и прилежащему острому углу).
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
3. Третий признак (по катету и противолежащему острому углу).
Если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и противолежащему острому углу другого прямоугольного треугольника, то такие треугольники равны.
4. Четвертый признак (по гипотенузе и острому углу).
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
5. Пятый признак (по катету и гипотенузе).
Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.