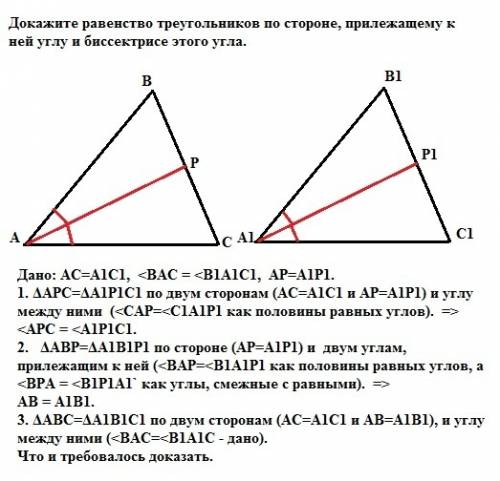
Дано: АС=А1С1, <BAC = <B1A1C1, АР=А1Р1.
1. ΔАРС=ΔА1Р1С1 по двум сторонам (АС=А1С1 и АР=А1Р1) и углу между ними (<CAP=<C1A1P1 как половины равных углов). => <APC=<A1P1C1.
2. ΔАВР=ΔА1В1Р1 по стороне (АР=А1Р1) и двум углам, прилежащим к ней (<ВAP=<В1A1P1 как половины равных углов, а <BPA = <B1P1A1` как углы, смежные с равными). => AB = A1B1.
3. ΔАВС=ΔА1В1С1 по двум сторонам (АС=А1С1 и АВ=А1В1), и углу между ними (<ВАС=<В1A1С - дано).
Что и требовалось доказать.
Проведем KO перпендикулярно плоскости ABCD
Проведем диагональ AС в ABCD
ABCD - квадрат(т.к пирамида правильная) ⇒ AB=BC=CD=AD
Рассмотрим ΔACD - прямоугольный
По теореме Пифагора:
AC²=AD²+CD²
Т.к. AD=CD Можно записать так:
AC²=2AD²
AC=√2AD²=√2*4²=√2*16=√32=4√2
AO=OC=2√2 - т.к. диагонали квадрата точкой пересечения делятся пополам
Рассмотрим ΔAOK - прямоугольный
По теореме Пифагора:
AK²=AO²+KO²
KO²=AK²-AO²
KO=√AK²-AO²=√17-8=√9=3
KO=H=3
Sосн=AD²=4²=16
V=Sосн*H/3=16*3/3=16
ответ: 16
(Я правильно понял, что боковое ребро равно √17?)