так будет легче объяснить
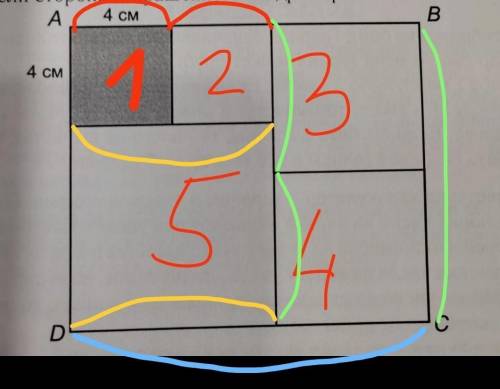
ответ : стороны квадрата 1 равны сторонам квадрата 2 суммируем две стороны получается прямоугольник со сторонами 4 и 8 см
сторона прямоугольника 1 равна стороне квадрата 5 так как у квадрата одинаковые стороны то складываем стороны 4 и 8 = 12 см получился прямокгольник со сторонами 8 и 12 см
квадраты 3 и 4 одна из их сторон равна 12
12÷2 =6 см у квадрата 3 и 4 стороны равны 6 см
и так знаем что это квадрат со сторонами 12 см и 12 см, периметр равен 12 ×4= 48 см
площадь равна 12×12 =144 см^2
Вычисления таких задач проще простого. Сумма углов треугольника равна 180 градусов, углы при основании (beta) равны. Отсюда на все случаи углов при вершине alpha следует применять формулу
beta=(180-alpha)/2.
Если угол при вершине 110 градусов, то у основания равнобедренного треугольника углы равны
beta=(180-110)/2=35 (градусов).
Пусть задан угол при основании равнобедренного треугольника и он равен 50 градусов, тогда угол при вершине равен
alpha=180-2*50=80 (градусов).
Меняете в формуле значения угла (50) на свой и находите угол в вершине треугольника для любого равнобедренного треугольника.
По мере изучения свойств треугольника, формулы для вписанных и описанных окружностей, возрастает и сложность вычислений и разнообразие задач, которые можно решить. Таким образом в 8-9 классе задачи на треугольники требуют знаний немало важных формул без которых вычисления невозможно выполнить.
Объяснение: