1см
Объяснение:
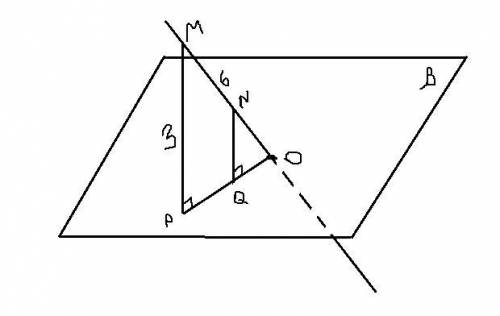
Точка N может лежать по одну сторону от плоскости β с точкой М или по другую. Если N лежит по другую сторону, то невозможно выполнить условия MN = 6 см и при этом OM = 9 см. Поэтому рассматриваем только случай, когда M и N находятся по одну сторону от плоскости β.
В этом случае расстояние от M до плоскости (определяется перпендикуляром, опущенным на эту плоскость) равно PM=3см. А расстояние от N до плоскости - QN.
Рассмотрим тр-ки MPO и NQO. Они подобны (2 угла прямые, а ещё один угол MOP общий). Значит PM/QN=OM/ON. ON=9-6=3
QN=PM*ON/OM=3*3/9=1
У меня получилось что расстояние от точки М до вершины В равно 8 см, показываю как получил:
1. СК и АN - медианы треугольника АВС.
2. По условию задачи точка М удалена от стороны АС на 4 см, то есть она принадлежит перпендикуляру, проведенному к стороне АС.
3. Проведем через эту точку высоту ВН к стороне АС.
4. По условию задачи треугольник АВС равнобедренный, следовательно, высота ВН является еще и медианой.
5. Точка пересечения медиан, согласно их свойствам, делит каждую из них на два отрезка, относящихся как 2 : 1, начиная от вершины, то есть ВМ : НМ = 2 : 1.
ВМ = 4 х 2 = 8 см.
ответ: расстояние от точки М до точки В равно 8 см.
Радиус вписанной окружности правильного треугольника, выраженный через его сторону
r = а √3:6
4 = а √3:6
а √3=4∙6
а=24:√3=24√3:3=8√3 см