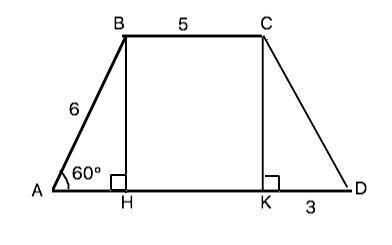
Условие дано неточно. ВН и СК не могут принадлежать АD, поскольку точки В и С принадлежат стороне ВС, которая параллельна АD. Правильно: АВСD – трапеция. АВ=6, ВС=5, KD=3, угол А = 60°. BH перпендикулярна AD, CK перпендикулярна AD. Найдите AD и Р(ABCD).
ответ: ВН - высота. Р(АВСD)= 28 (ед. длины)
* * *
а) Отрезок ВН опущен из вершины трапеции на ее основание, перпендикулярен ему и является её высотой.
б) Так как угол ВНА=90°, треугольник АВН - прямоугольный. Сумма острых углов прямоугольного треугольника 90° => угол АВН=30°. Катет АН противолежит углу 30° и равен половине гипотенузы АВ ( свойство). АН=6:2=3.
Четырехугольник НВСК - прямоугольник, т.к его углы прямые. Противоположные стороны прямоугольника равны. НК=ВС=5. и СК=ВН. Рассмотрим ∆ СКD. Катет СК=ВН, катет КD=AH (найдено). ∆ СКD=∆АВН по двум катетам. => СD=АВ=6.
АD=AH+HK+KD=3+5+3=11
Р(ABCD)=AB+BC+CD+AD=6+5+6+11=28.
Объяснение: В ΔМNK из точки М проведите дугу окружности так, чтобы пересечь прямую NK в двух точках Р и Q. Затем поочереди из двух точек Р и Q проведите дуги одинакового радиуса на полу- плоскости относительно прямой NK, где нет точки М. Назовём точку пересечения этих дуг точкой А. Соединим М и А, получим МН ⊥ NK.
Описание: 1) окр (М; r) ∩ MK, получим Р и Q.
2) окр (Р; R) ∩ окр (К; R) = А.
3) МА ∩ NK = Н, МН- искомая высота Δ МNК.
В ΔСДР проведём поочерёдно две дуги одинаковым радиусом больше половины отрезка ДР навстречу друг другу из точек Д и Р. Эти дуги пересекутся в двух точках М и N. Соединим отрезком точки М и N.
Точку пересечения МN и ДР обозначим точкой К. Проведём отрезок СК, который и будет медианой ΔСДР.
Описание: 1)окр (Д; R) ∩ окр(Р; R), получим М и N.
2) MN ∩ ДР = К, СК- искомая медиана ΔСДР.
P.S. Если непонятно обозначение окружности в описании, то:
окр ( Р; R) - обозначение окружности с центром в Р и радиусом R.