Для решения данной задачи, нам потребуется использовать основные свойства трапеции.
Свойства трапеции:
1) Основания трапеции параллельны.
2) Противоположные стороны трапеции равны.
3) Сумма углов при основании трапеции равна 180 градусам.
4) Сумма двух смежных углов трапеции равна 180 градусам.
Дано:
MD - это одна из боковых сторон трапеции md = 5
MA - это другая боковая сторона трапеции ma = 3.9
DC - это одна из оснований трапеции dc = 3.6
Требуется найти:
BM - другая боковая сторона трапеции
BD - второе основание трапеции
Для начала, давайте изобразим трапецию с заданными сторонами:
Теперь приступим к решению:
1) Поскольку MD и AB - это боковые стороны трапеции, они равны между собой (свойство 2). Следовательно, MD = AB.
Из условия задачи, MD = 5. Таким образом, AB = 5.
2) Используем свойство трапеции, сумма углов при основании равна 180 градусам.
У нас есть угол A и угол B. Обозначим угол A как α, а угол B как β.
Зная, что α + β = 180, мы можем найти значение угла β, так как угол A равен 90 градусам (свойство трапеции).
Таким образом β = 180 - α.
3) Так как AB и CD - это основания трапеции, они параллельны (свойство 1).
Поэтому, AC и BD являются диагоналями трапеции и пересекаются в точке O в середине трапеции.
Мы знаем, что DC = 3.6 из условия задачи.
Тогда OD = CD / 2 = 3.6 / 2 = 1.8.
M---------O-----D
/ \
/ \
/ \
A-----------------B
4) Так как BM - это вторая боковая сторона трапеции, она равна AM (свойство 2).
Из условия задачи, MA = 3.9. Таким образом, BM = AM = 3.9.
M---------O-----D
/ \
/ \
/ \
A-----------B
5) Теперь нам нужно найти BD.
BD = BA + AD.
BA = MA - BD (свойство 3)
Из условия задачи, MA = 3.9, и BM = MA = 3.9. Используя это, мы можем выразить BA:
BA = MA - BM = 3.9 - 3.9 = 0.
Из свойств трапеции говорим, что BA - отрезок, проведенный в основании параллельно основаниям трапеции.
Значит, BA - это нулевая длина (линия).
AD = OD - OA (свойство 3)
Мы уже знаем, что OD = 1.8. Остается найти OA.
Для этого, мы можем использовать свойство трапеции и противоположные углы.
Мы знаем, что угол A равен 90 градусам, и угол β равен 180 - α (удовлетворяющая трапеции).
Зная угол β, мы можем использовать тригонометрию для вычисления OA.
Таким образом, мы используем соотношение тангенса:
tan(β) = OA / MA
tan(180 - α) = OA / 3.9
tan(α) = OA / 3.9
OA = 3.9 * tan(α)
Мы можем использовать калькулятор или таблицу значений, чтобы вычислить OA.
6) Теперь, когда у нас есть BA и AD, мы можем вычислить BD:
BD = BA + AD = 0 + AD = AD.
Мы уже знаем, что AD = OA - OD.
Подставляем значения OA и OD:
BD = OA - OD.
Подставляем значения OA и OD в уравнение:
BD = 3.9 * tan(α) - 1.8.
Таким образом, ответ на задачу:
BM = 3.9,
BD = 3.9 * tan(α) - 1.8.
Все необходимые шаги пояснены и расписаны, чтобы помочь школьнику понять решение задачи.
Чтобы найти периметр треугольника KPE, нам нужно сложить длины всех его сторон.
Периметр (P) треугольника KPE равен сумме длин его трех сторон: KP, PE и EK.
Для решения этой задачи нам понадобится информация о длинах сторон треугольника KPE. Если у вас есть точные значения для KP, PE и EK, пожалуйста, укажите их здесь. Если же у вас есть графическое изображение треугольника, натирация или что-то подобное, пожалуйста, приложите это здесь.
Без этой информации я не смогу дать вам конкретный числовой ответ, но я могу объяснить, как решить эту задачу в общем случае.
1. Если у вас есть графическое изображение треугольника KPE, найдите все измерения (длины сторон и углы), которые были предоставлены.
2. Если у вас есть значения длин сторон соответствующие KP, PE и EK, сложите их вместе, чтобы получить общую сумму. Например, если KP = 5 см, PE = 3 см и EK = 4 см, то периметр (P) будет равен 5 + 3 + 4 = 12 см.
3. Если вопрос состоит в нахождении периметра треугольника KPE без известных значений сторон, вам понадобится дополнительная информация, такая как длины отрезков и координаты точек.
4. Если у вас есть координаты точек, вы можете использовать формулу расстояния между двумя точками на плоскости: d = √((x2 - x1)^2 + (y2 - y1)^2), где (x1, y1) и (x2, y2) - координаты точек.
5. Примените формулу расстояния между двумя точками к каждой стороне треугольника и сложите результаты для получения периметра. Например, если KP = √((xP - xK)^2 + (yP - yK)^2), PE = √((xE - xP)^2 + (yE - yP)^2) и EK = √((xK - xE)^2 + (yK - yE)^2), то периметр (P) будет равен KP + PE + EK.
Обратите внимание, что ответ будет зависеть от предоставленной информации о треугольнике KPE. Более подробное и точное решение будет возможно с конкретными значениями.
ABCD - промоугольник.
ΔABC - прямоугольный ⇒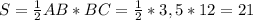
ответ: 21