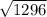 =36
=36Объяснение:
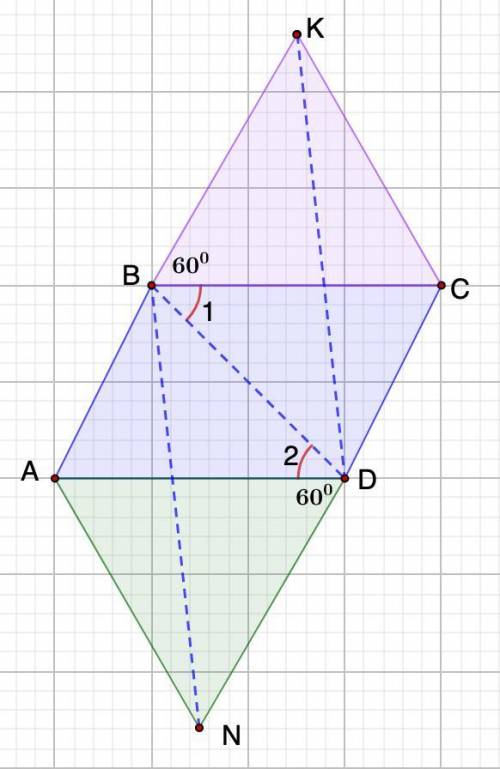
Дано: ABCD - параллелограмм.
ΔВКС и ΔAND - равносторонние.
Доказать: BKDN - параллелограмм.
Доказательство:
1. Рассмотрим ΔВКС и ΔAND - равносторонние.
Противоположные стороны параллелограмма равны.⇒ ВС = AD
⇒ ΔВКС = ΔAND (по трем сторонам, 3 признак)
⇒ BK = ND
2. ВС || AD (ABCD - параллелограмм)
∠1 = ∠2 (накрест лежащие при ВС || AD и секущей BD)
В равностороннем треугольнике углы равны 60°.⇒
∠DBK = ∠1 + 60°
∠BDN = ∠2 + 60°
⇒ ∠DBK + ∠BDN - накрест лежащие при BK и ND и секущей BD.
Если при пересечении двух прямых третьей накрест лежащие углы равны, то прямые параллельны.⇒ BK || ND
Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник - параллелограмм.⇒ BKDN — параллелограмм
углы параллелограмм =УглыA+B+C+D=360
пусть угол А =С=х
пусть угол В=D=x+30
x+x+30+x+x+30=360
4x=360-60
4x=300
x=300/4
x=75
значит углы А =С равен 75
углы В=D равен 75+30=105