Площадь параллелограмма вычисляется по формуле:
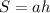 , где а - сторона параллелограмма, h - высота, проведенная к этой стороне.
, где а - сторона параллелограмма, h - высота, проведенная к этой стороне.
Площадь прямоугольника вычисляется по формуле:
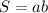 , где a,b - стороны прямоугольника.
, где a,b - стороны прямоугольника.
Прямоугольником называется параллелограмм, у которого все углы прямые, тогда сторону b можно определить как высоту, проведенную к стороне a, значит, если в параллелограмме и прямоугольнике найдется по равной стороне и высота в параллелограмме, проведенная к этой стороне, будет равна второй стороне прямоугольника, такие параллелограмм и прямоугольник будут иметь одинаковые площади.
Площадь поверхности призмы = площадь боковой поверхности + 2 х площадь основания
а - сторона основания
площадь в правильном треугольнике = (а в квадрате х корень3)/4
т.к. имеется два основания то площади оснований = (а в квадрате х корень3)/2
площадь боковой поверхности = 3 х (площадь боковой грани)
площадь боковой грани = сорона основания х высоту
площадь боковой грани = 3 х (а х 2 х корень3) = 6а х корень 3
Площадь поверхности призмы = (а в квадрате х корень3)/2 + 6а х корень 3
14 х корень3 =(а в квадрате х корень3)/2 + 6а х корень 3
а в квадрате +12а =28
далее решается как квадратное уравнение
а в квадрате +12а - 28=0
а = (-12 +-(плюс, минус) корень(12в квадрате - 4 х 1 х (-28))/ 2х1
а= (-12 +-(плюс, минус) корень (144 + 112))/2
а = (-12 +16)/2
а =4/2=2
второй коррень невозможен т.к он отрицательный
сторона треугольника =2
Диагональ= корень(сторона треуг. в квадрате + высота в квадрате) = корень (4+12) = 4
Найдем высоту АН этого параллелограмма, проведенную к стороне DС из вершины А.
Треугольник ADH- прямоугольный.
АН=АD*sin (60°)=(3х√3):2
Площадь АВСD=АН*DC
45√3=[(3х√3):2]*10х
45=15х²х²=3
х=√3
AD=3√3 cм
Проведем прямую МК, параллельную АD.
АD=АК, так как угол КАМ=углу АМD по свойству углов при пересечении двух параллельных прямых секущей.
AD=KM, AK=AD ⇒
АКМD - ромб со сторонами 3√3 а, поскольку острые углы этого ромба равны 60°, угол DAK=120°, угол DAM=60°, треугольник АDM - равносторонний и
АМ =AD= 3√3 cм