Две различные прямые либо имеют только одну общую точку, либо не имеют ни одной общей точки. В первом случае говорят, что прямые пересекаются, во втором случае — прямые не пересекаются.
Две прямые на плоскости называются параллельными, если они не пересекаются.Если при пересечении двух прямых секущей:
накрест лежащие углы равны, илисоответственные углы равны, илисумма односторонних углов равна 180°, то прямые параллельныЕсли две параллельные прямые пересечены секущей, то:
накрест лежащие углы равны;соответственные углы равны;сумма односторонних углов равна 180°.
Первое решение полное и понятное. Если не помните формулу Герона, есть
Вариант решения ( без формулы Герона).
Формула радиуса описанной окружности
R=a•b•c/4S, где а, b, и с - стороны треугольника
S-a•h
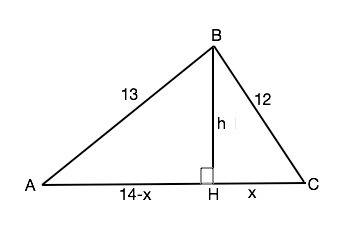
Проведем к большей стороне АС высоту ВН.
Примем СН=х
Тогда АН=14-х
По т.Пифагора
ВН²=АВ²-АН² =169-196+28х-х²
ВН²=ВС²-СН²=144-х²
Приравняем значения квадрата высоты:
169-196+28х-х²=144-х², откуда
28х=171
х=6,107
ВН=√(144-37,3)=√106,7=10,33
S=10,33•14/2=72,31
R=12•13•14/4•72,31=546/72,3= ≈7,55 см
sinA=BH/АВ==10,33/13= ≈0,7946
∠А≈52°36'
если сделал(А) чертеж то видно, что площади треугольников равны половине высота(радиуса)*сторону основания. 0.5a*r=120 0.5b*r=104 0.5c*r=112. выражаем стороны. a=240/r b=208/r c=224/r . формула герона :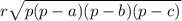
где p - полупериметр((a+b+c)/2). подставляем значиения a, b и c, выносим из под корня число и получаем 
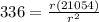сокращаем r и умножаем обе части на r => 336r=21054, делим на 336 и получаем ответ: 64