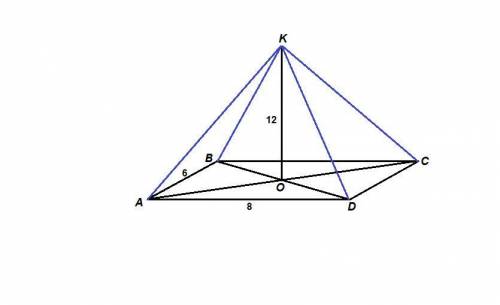
KA = KB = KC = KD = 13
Объяснение:
Из прямоугольного треугольника АВС находим АС по теореме Пифагора:
АС = √(АВ² + ВС²) = √(36 + 64) = 10
Диагонали прямоугольника равны и точкой пересечения делятся пополам:
АО = ВО = СО = DO = 5
АО, ВО, СО и DO - проекции наклонных KA, KB, KC и KD на плоскость прямоугольника.
Если равны проекции наклонных, проведенных из одной точки, то равны и сами наклонные, т.е.
KA = KB = KC = KD.
Из прямоугольного треугольника АОК по теореме Пифагора находим КА:
КА = √(ОК² + АО²) = √(12² + 5²) = √(144 + 25) = √169 = 13
KA = KB = KC = KD = 13
1. Тут можно много решений сделать, но вообще то задача устная.
Если взять куб со стороной 3 - пусть это ABCDA1B1C1D1, провести диагонали граней А1В и А1D, они как раз и будут такими наклонными к плоскости основания ABCD. Все что надо сообразить - что треугольник А1ВС равносторонний, поэтому угол между А1В и А1С равен 60 градусам. Понятно, что проекции диагоналей - это строны квадрата в основании. То есть выполнены все условия задачи. (Можно считать, что я "достроил" фигуру из наклонных и проекций до куба с сечением по двум пересекающимся диагоналям смежных граней)
Теперь очевидно, что расстояние от А1 до основания ABCD равно стороне куба 3.
2. Поскольку точка М равноудалена от сторон треугольника, то и её проекция - точка О равноудалена от сторон, то есть эта проекция - центр вписанной окружности. Если через точку М провести плоскость перпендикулярно одной из сторон - например АВ, то эта плоскость очевидно пройдет через О (МО - перпендикуляр к плоскости треугольника). Если обозначить за К точку пересечения этой плоскости со стороной АВ, то треугольник МОК прямоугольный, МО = 1, МК = 2 (ясно, что МК перпендикулярно стороне АВ). Отсюда угол МКО = 30 градусов.
Второй катет, который очевидно равен √3 - это радиус вписанной в АВС окружности. Отсюда легко сосчитать, что высота треугольника равна 3√3, а сторона равна 6.
(В правильном треугольнике центры вписанной и описанной окружностей совпадают с точкой пересечения медиан, то есть r = h/3; R = 2h/3; h = a√3/2)
y=kx+b
1)-0,5, 2,5
2)b=7,k=2
3)-0,6;2,8
Объяснение:
-1)-2y=x+5
y=-x+5/2
,y=-x/2+2,5,k=-0,5,b=2,5
2)1=2×(-3)+b, -6+b=1 b=7
3)x-x1/x2-x1=y-y1/y2-y1, y=-0,6x+2,8, k=-0,6, b=2,8
4)AB.y=x-2, k=1,b=-2
BC.y=6x/7-11/7, k=6/7, b=-11/7
AC.y=11x/12-13/6, k=11/12, b=13/6