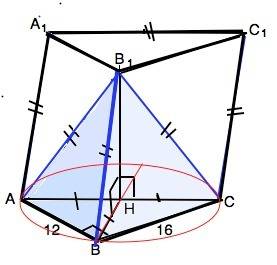
Грань АА1С1С - квадрат.
АС по т.Пифагора равна 20. В призме все боковые ребра равны. ⇒ ВВ1=СС1=АА1=АС=20.
По условию боковые ребра пирамиды АВ1СВ равны, значит, их проекции равны между собой и равны радиусу окружности, описанной около основания АВС. ⇒
Вершина пирамиды В1 проецируется в центр Н описанной около прямоугольного треугольника окружности, т.е. лежит в середине гипотенузы.
∆ АВС прямоугольный, R=АС/2=10.
АН=СН=ВН=10.
Высота призмы совпадает с высотой В1Н пирамиды.
По т.Пифагора
В1Н=√(BB1²-BH²)=√(20²-10²)=√300=10√3
Формула объёма призмы
V=S•h где S - площадь основания, h - высота призмы.
S-12•16:2=96 (ед. площади)
V=96•10√3=960√3 ед. объёма.
1) центральным углом в окружности называется плоский угол с вершиной в её центре.
2) дуга
3) ∪
4) когда дуга принадлежит центральному углу
5) 360°
6) центральный угол равен дуге, на которую он опирается
7) хорда стягивает 2 дуги и их градусная мера равно 360°
8) угол вершина которого лежит на окружности, а стороны пересекают окружность
9) в том случае если она лежит внутри угла
10) градусная мера врисанного угла равна половине дуги, на которую он опирается.
11) выписаные углы опирающиеся на одну и ту же дугу - равны.
12) прямой