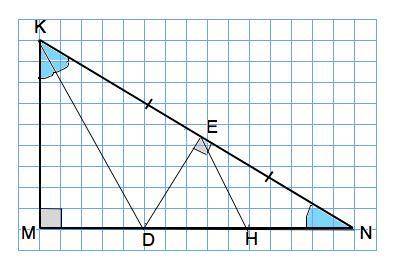
В ∆ KDN отрезок DE - высота, а т.к. KЕ=EN, то и медиана.
Следовательно, ∆ KDN - равнобедренный, углы DKN=KND.
Угол NKD= углу MKD Поэтому угол МКN=2 угла N.
Сумма острых углов прямоугольного треугольника 90°.
3N=90° => Угол N=30°.
В прямоугольном ∆ DЕN проведем медиану ЕН.
По свойству медианы прямоугольного треугольника ЕН=DH=HN, треугольник ЕНN и треугольник DEH- равнобедренные. Угол HED=ЕDN=90°-30°=60°, ∆ DEH – равносторонний.
Точка D по свойству биссектрисы равноудалена от сторон КМ и КN.
МD=DE, а DE=DH=HN => MD=HN => MN=3MD. Доказано.
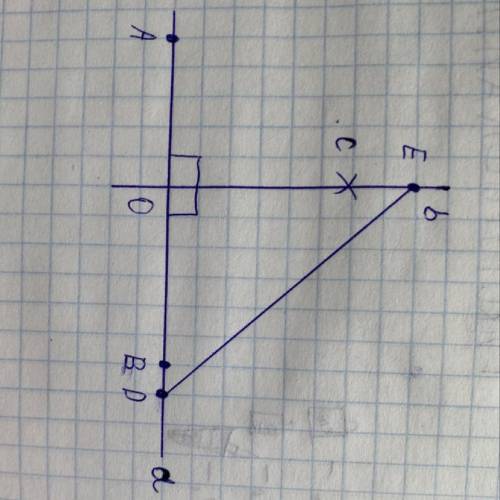
Медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины. ⇒
АЕ=2/3 медианы из вершины А.
Проведем через Е прямую параллельно СВ.
К - точка ее пересечения с АС.
Треугольники АКЕ и АСМ подобны - прямоугольные с общим углом А.
Из подобия следует, что КЕ делит АС в отношении АЕ:ЕМ, т.е. 2:1⇒
АК=8, КС=4
КЕ:СМ=АК:АС
КЕ:(9:2)=8:12
КЕ=36:12=3
Точка пересечения биссектрис треугольника является центром вписанной в него окружности.
Радиус вписанной в прямоугольный треугольник окружности можно найти по формуле:
r=(a+b-c):2
Треугольник АВС - египетский ( отношение катетов 3:4) ⇒
АВ=15 ( ту же длину гипотенузы АВ получим по т.Пифагора)
r=(12+9-15):2=3
Расстояние от любой точки биссектрисы треугольника до его сторон одинаково.
Расстояние от О до катетов равно r=3 ⇒
ТО=СН=ОН=3
Но КЕ=3 (см. выше)
Четырехугольник СКЕН - прямоугольник
ЕН=КС=4
ОЕ=ЕН-ОН=4-3=1 см