ответ: 69
Объяснение:
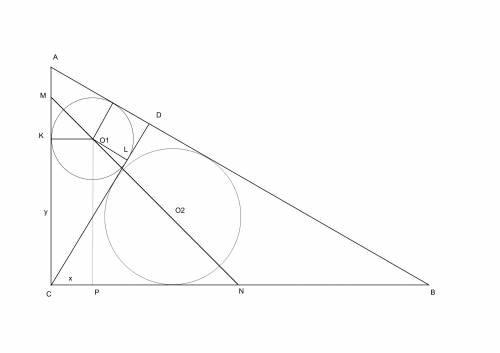
Если внимательно посмотреть на чертеж, то сразу видно, что CP + CK = CD; так как CP = KO1 = r = LD; CK = CL;
Обозначая CK = y; CP = x; CD = h (высота ABC), я получаю для точки O1
x + y = h;
Аналогично можно показать то же самое для центра второй окружности O2;
То есть если считать катеты осями прямоугольной системы координат, то уравнение прямой O1O2 так и будет x + y = h;
(прямая с таким уравнением проходит через эти две точки, а через две точки можно провести только одну прямую)
Это прямая, пересекающая оси под углом в 45 градусов, в точках (0, h) и (h, 0).
Отсюда следует, что треугольник CMN - равнобедренный, с катетами CM = CN = CD = h и площадью h^2/2;
Подставляя значения из условия, легко найти
h^2 = 18*2 = 36; h = 6;
Sabc = 23*6/2 = 69;
1). На произвольной прямой отложить отрезок, равный стороне АВ. Обозначить на концах отрезка вершины треугольника: точки А и В.
2) Из точки А как из центра раствором циркуля радиусом, равным длине стороны АС, начертить дугу.
3) Из т.В как из центра раствором циркуля радиусом, равным длине стороны ВС, начертить дугу до пересечения с первой дугой.
Точка пересечения дуг – вершина С искомого треугольника. Соединив А и С, В и С, получим треугольник со сторонами заданной длины.
б) Построение срединного перпендикулярна стандартное.
Из т.А и т.В как из центров провести полуокружности произвольного, но равного радиуса несколько больше половины АВ так, чтобы они пересеклись по обе стороны от АВ (т.К и т. Н).
Точки пересечения К и Н этих полуокружностей соединить.
Соединить А и Н, В и Н. Четырехугольник АКВН - ромб ( стороны равны взятому радиусу). Диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам. =>
АМ=МВ и КМ перпендикулярно АВ.
КМ - срединный перпендикуляр к стороне АМ.
Точно так же делят отрезок пополам.