Значит, необходимо найти длину отрезка AB.
Пусть окружность лежит в плоскости α.
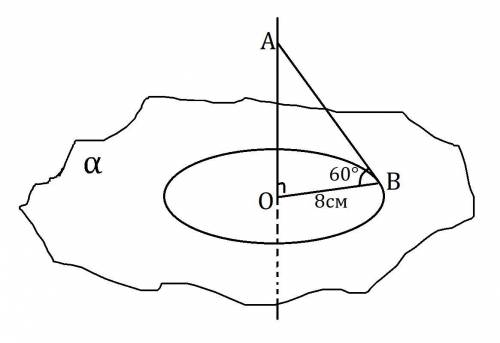
OB = 8см, как радиус окружности (O - центр, B - точка окружности).
AO⊥α, OB⊂α ⇒ AO⊥OB ⇒ ΔAOB - прямоугольный (∠O=90°).
Сумма углов треугольника равна 180°.∠OAB + ∠AOB + ∠ABO = 180°;
∠OAB + 90° + 60° = 180°;
∠OAB = 180°-150° = 30°.
Катет, лежащий напротив угла в 30°, вдвое меньше гипотенузы.OB - катет, лежащий напротив ∠OAB=30°; AB - гипотенуза.
OB·2 = AB;
AB = 8см·2 = 16см.
ответ: 16см.
Площа трикутника за найпоширенішою формулою рівна половині добутку основи на висоту, проведеної до неї. Виконуємо обчислення
S= 24*16/2=192 (кв. см.)
Для визначення периметру нам потрібно відшукати довжину бічної сторони.
У рівнобедреному трикутнику висота, проведена до основи в, є бісектрисою і медіаною.
За теоремою Піфагора знаходимо бічну сторону трикутника
b=sqrt(16^2+(24/2)^2)=20 (cм)
Периметр - сума всіх сторін
P= 2*20+24=64 (см)
Знаходимо радіус вписаного в трикутник кола за формулою
r=S/(2*P)=192/(64/2)=192/32=6 (см).
ЗАДАЧА 2 Основа рівнобедреного трикутника дорівнює 24 см бічна сторона 13 см. Обчисліть площу трикутника?
Розв'язання: Площа рівна пів добутку основи на висоту.
Основа нам відома, висоту знаходимо за теоремою Піфагора
h=√(b²-a²/4)= √(169-144)=5 (см).
Далі обчислюємо площу
S=a*h/2=24*5/2=60 (см. кв.)
Объяснение: