1.
М - середина АВ, значит МВ = АВ/2
Р - середина МВ, значит РВ = МВ/2 = АВ/4
К - середина ВС, значит КС = ВС/2
Е - середина КС, значит ЕС = КС/2 = ВС/4
N - середина АС, значит NA = АС/2
G - середина NA, значит GA = NA/2 = AC/4
По условию
PB + EC + GA = 12
АВ/4 + ВС/4 + АС/4 = 12
1/4 · (АВ + ВС + АС) = 12
АВ + ВС + АС = 12 · 4 = 48 (см)
2.
Из решения первой задачи следует, что
АР = 3/4 АВ
ВЕ = 3/4 ВС
CG = 3/4 AC
По условию
AP + BE + CG = 108
3/4 АВ + 3/4 ВС + 3/4 АС = 108
3/4 · (АВ + ВС + АС) = 108
АВ + ВС + АС = 108 · 4/3 = 144 (см)
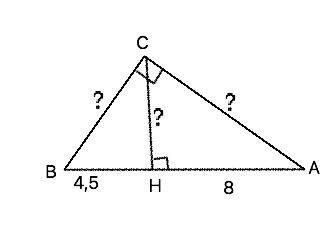
В прямоугольном треугольнике высота из прямого угла перпендикуляр, катеты - наклонные, а отрезки гипотенузы, на которые делит ее высота – проекции катетов на нее. На предлагаемом в приложении рисунке ВН - проекция катета ВС и АН - проекция катета АС на гипотенузу.
Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее геометрическое (среднее пропорциональное) между проекциями катетов на гипотенузу. ⇒ СН=√(BH*AH)=√(4,5•8)=6 см
Катет прямоугольного треугольника есть среднее геометрическое (среднее пропорциональное) между гипотенузой и проекцией этого катета на гипотенузу Гипотенуза АВ=8+4,5=12,5. ⇒ BC=√(AB•BH)=√(12,5•4,5)=7,5 см АС=√(AB•AH)=√(12,5•8)=10 см.
* * *
Т.к. высота прямоугольного треугольника делит его на подобные, те же результаты будут получены при решение через подобие треугольников.
сумма углов чётырёхугольника равна 360 градусов
угол АСД = 360-(43+137+45)=135
ответ 135 градусов