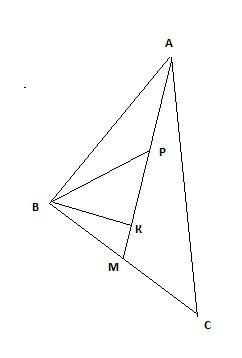
Построим треугольник АВС, площадь которого равна 40 кв. см, Проведем медиану АМ. и обозначим точу Р такую, что АР:РМ=2:3.
Так как медиана треугольника делит его на две равновеликие части, то Sавм=40/2=20 кв. см.
Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты).
Для наглядности построим высоту ВК – она будет являться высотой как для треугольника ВАМ так и для треугольника ВРМ
Основания Данных треугольников будут соотноситься как 3:5, значит
Sврм : Sвам=3 : 5
Sврм= Sвам*3 / 5=20*3/5=12 кв.см.
ответ: Б)
Объяснение: (к сожалению, сейчас нет возможности добавить рисунок)
Vпризмы = Sосн * АА1
если обозначить сторону основания (для удобства) (а), то Sосн = а^2*√3/4;
по условию cos(ACA1) = 1/3 = cos(ABA1); sin(ACA1) = √(1-(1/9)) = √8/3; tg(ACA1) = √8 и потому высота призмы АА1 = a*√8
Vпризмы = а^3*√3/√2
сечением будет равнобедренный треугольник СА1В, СА1=ВА1=3а; СВ=а
и его площадь известна...
мне нравится формула Герона...
4√35 = √(3.5а*0.5а*0.5а*2.5а)
100*4√35 = а^2*√(35*5*5*25)
100*4√35 = 25а^2*√35
а^2 = 16
а^3 = 64
Vпризмы = 64*√3/√2 = 32√6
Р = 2×(70+410) = 2 × 480 = 960 м
2) т.к. Р(прямоугольника) = Р(квадрата) по условию задачи, найдем сторону квадрата через формулу периметра:
Р = 4а
4а = 960
а = 960 ÷ 4
а = 240 м
3) Найдем площадь прямоугольника и квадрата и сравним их:
S(прямоугольника) = a×b = 70×410 = 28700 м^2
S(квадрата) = а^2 = 240^2 = 57600 м^2
4) S(квадрата) > S(прямоугольника) на:
57600 - 28700 = 28900 м
ответ: площадь участка квадратной формы больше на 28900 м