Так как АВ и CD - это диаметры окружности, то точкой О они делятся пополам. Тогда АО = ОВ = СО = ОD = АВ/2 = CD/2.
АВ = 12, тогда: АО = ОВ = СО = ОD = 12/2 = 6 (см).
Углы СОВ и АОD равны, так как являются вертикальными углами, образованными пересечением двух прямых.
Рассмотрим два треугольника СОВ и АОD: угол СОВ = угол АОD, АО = ОВ = СО = ОD = 6 см. Треугольники СОВ и АОD равны по двум сторонам и углу между ними. Тогда AD = CB = 10 см.
Периметр треугольника АОD:
Р = АО + ОD + АD;
Р = 6 + 6 + 10 = 22 (см).
ответ: Р = 22 см.
Объяснение:
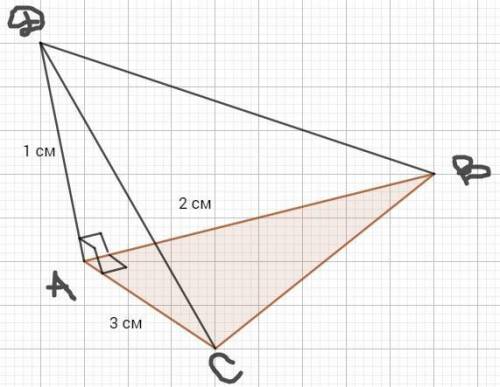
Из ΔАВС (∠А = 90°): ВС = √(АВ² + АС²) = √(9 + 4) = √13 см
Из ΔАDВ (∠А = 90°): ВD = √(АВ² + АD²) = √(1 + 4) = √5 см
Из ΔАDC (∠А = 90°): CD = √(АC² + АD²) = √(9 + 1) = √10 см
Площадь ΔDВС найдём по формуле Герона
S = √(p(p - DВ)(p - DС)(p - BC)), p = (DВ + DС + BC) : 2 = (√5 + √10 + √13) : 2 см
S = √((√5 + √10 + √13) : 2((√5 + √10 + √13) : 2 - √5)((√5 + √10 + √13) : 2 - √10)((√5 + √10 + √13) : 2 - √13)) = √((√5 + √10 + √13) : 2((√10 + √13 - √5) : 2)((√5 + √13 - √10 ) : 2)(( √5 + √10 - √13) : 2)) =0,25√((√5 + √10 + √13)(√10 + √13 - √5)(√5 + √13 - √10)( √5 + √10 - √13))=0,25√((√13 + √10)² - 5)(√5 + √13 - √10)( √5 - (√13 - √10))=0,25√((√13 + √10)² - 5)( 5 - (√13 - √10)²)=0,25√((13 + 10 + 2√130 - 5)( 5 - 13-10 + 2√130))=0,25√((18 + 2√130)(2√130-18))=0,25√(4·130 - 324)= 0,25√(520 - 324)= 0,25√196 = 0,25·14 = 3,5 см².
Можно ещё через высоты треугольников площадь вычислить, а также с использованием формулы площади ортогональной проекции. Я выбрал формулу Герона, чтобы показать как можно преобразовывать иррациональные выражения.
24
Объяснение:
0,15х - 0,6 = 9,9 - 0,3x + 0,3
0,15x + 0,3x = 9,9 + 0,3 + 0,6
0,45x = 10,8
x = 10,8 : 0,45
x = 24