телом вращения является два усеченных конуса S=S1+S2
1) S=π (r12+(r1+ r2) l+ r22)
проведем АР -перпендикуляр к КМ -оси вращения АР=r1 усеченного конуса , АВ - его образующая
из треугольника АВС найдем r1= АР1+Р1Р
ha= 2sqrt ( p (p−a) (p−b) (p−c) ) / a
AP1 = 12cm
r1= 12+3=15cm r2=3cm
S1=900π
S2=468π
S=1368π cm^2
2)V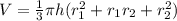
V=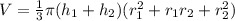
V= 3720 π cm^3

Объяснение:
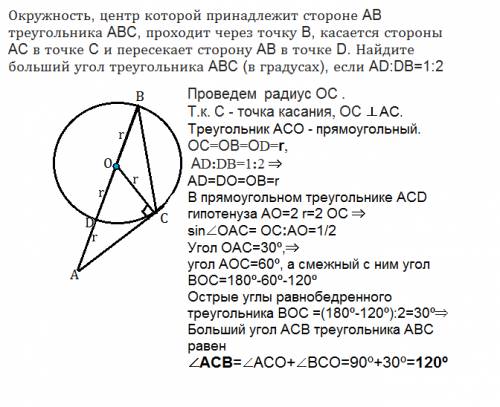
Из условия нам известно, что ∠DOC равен пяти углам COB.
Если посмотреть на чертеж, то мы увидим, что ∠DOC и ∠COB смежные, а следовательно, их сумма равна 180°. Для нахождения углов DOC и COB составим линейное уравнение:
Пусть x - ∠DOC, тогда ∠COB - 5x. (угол COB равен 5x, т.к. он в 5 раз больше угла DOC)
Получаем:
x + 5x = 180°
6x = 180°
x = 30° (Это мы нашли x, то есть ∠DOC)
∠COB = 30° * 5 = 150°.
Ну а дальше - дело техники.
∠COD = ∠BOA = 150°(все вертикальные углы равны)
∠BOC = ∠AOD = 30°(все вертикальные углы равны).
Задача решена.
объем тела вращения = 2250*п
площадь поверхности тела вращения = 3п * (2+125корень(3))