Задача решена Пользователем Рисадес Хорошист
Исправлена неточность в последнем действии.
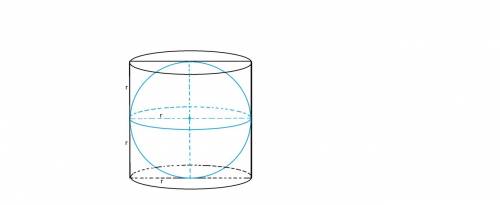
Шар может быть вписан в цилиндр только тогда, когда этот цилиндр правильный, т.е. когда его осевое сечение является квадратом.
Радиус основания цилиндра равен радиусу шара и равен r.
Высота цилиндра равна диаметру основания и равна 2 r.
Полная площадь поверхности складывается из площади двух оснований и площади боковой поверхности:
2*πr² + 2πr*2r = 6πr²
Площадь шара = 4πr²
Площадь цилиндра больше площади шара в
6πr² : 4πr² = 1,5 (раза)
Площадь полной поверхности шара
111 : 1,5 = 74 ( единиц площади)
Высота, опущенная на гипотенузу, связана с катетами прямоугольного
треугольника соотношением:
1/a²+1/b²=1/h² или h²=a²*b²/(a²+b²) или h²=a²*b²/с².
Или h=a*b/c.
В нашем случае h=10*24/26=120/13.
Тогда площадь трапеции равна S=(4+22)*120/2*13=120cм².
ответ:S=120cм².
P.S. Заметим, что площадь трапеции S=(BC+AD)*h/2 равна площади прямоугольного треугольника АСЕ, так как высота у них одинакова, а основание (гипотенуза) треугольника равна сумме оснований трапеции:
Sace=AE*h/2=(BC+AD)*h/2. Таким образом, можно было не находить высоту трапеции, а площадь ее найти как половину произведения диагоналей трапеции (катетов треугольника), то есть
S=AC*BD/2=10*24/2=120см².
Или найти площадь треугольника АСЕ (равную площади трапеции ABCD) по формуле Герона (для любителей корней):
S=√[p(p-a)(p-b)(p-c)]=√(30*20*6*4)=120см².