Объяснение:
Итак, когда секущая пересекает параллельные прямые, образуется несколько видов углов:
1) Внутренние накрест лежащие (которые равны)
2) Внутренние односторонние углы(их сумма составляет 180 градусов)
3) Соответственные углы(они равны)
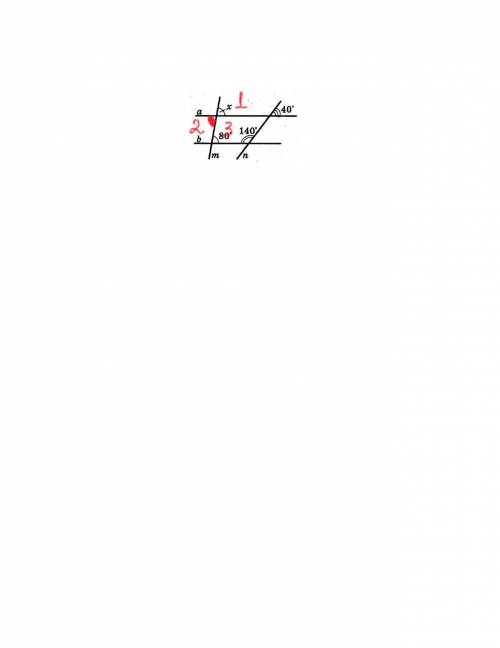
Я отметил на рисунке угол x как угол 1.
Угол 1 будет равен углу 2, т.к. они вертикальные, а это значит, что угол 2 будет равняться x.
А угол 3(который имеет градусную меру в 80 градусов) будет равен углу 2, так как они накрест лежащие. А это значит, что угол x будет равен 80 градусов.
Задача решена.
Проведем высоту через точку пересечения диагоналей.
Высота делит основания равнобедренной трапеции пополам.
Пусть отрезок высоты в треугольнике ВОС равен х, а отрезок высоты в треугольнике AOD равен (h-x).
BC/2=x·tg((180°-α)/2)
AD/2=(h-x)· tg((180°-α)/2)
Средняя линия трапеции равна полусумме оснований.
MN=(BC+AD)/2=(BC/2)+(AD/2)=x·tg((180°-α)/2) +(h-x)· tg((180°-α)/2) =
=tg((180°-α)/2)(x+h-x)=h·tg((180°-α)/2)=h·tg(90°-(α/2))