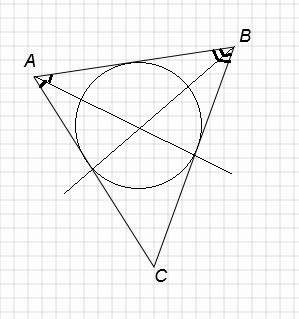
а) центром окружности, вписанной в треугольник является точка пересечения биссектрис (достаточно провести две) см. приложение
б) центром окружности, описанной около треугольника является точка пересечения серединных перпендикуляров к его сторонам (достаточно провести два) см. приложение
в) вневписанных окружностей у треугольника три - у каждой стороны своя окружность,центр каждой лежит на пересечении биссектрисы одного внутреннего угла и биссектрис внешних углов при двух других вершинах (достаточно провести два) см. приложение. не забудь дочертить ещё две к другим сторонам

Докажите, что медиана треугольника делит его на два треугольника, площади которых равны между собой.
Решение:
Проведем высоту из точки B. Высота BE - общая высота для треугольников BAD и BCD.
SBAD=BE*AD/2
SBCD=BE*DC/2
AD=DC (по определению медианы)
SBAD/SBCD=(BE*AD/2)/(BE*DC/2)=BE*AD/BE*DC=AD/DC=1
SBAD=SBCD
Что и требовалось доказать (ч.т.д.)