Смотри рисунок к задаче в прикрепленном файле.
Вершины четырехугольника делят окружность на дуги. Обозначим одну часть через х°.
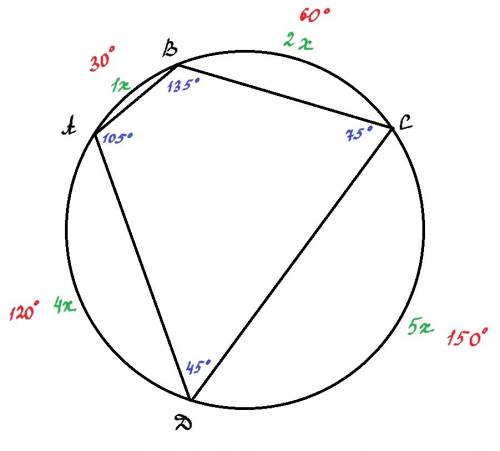
Тогда градусная мера дуги АВ=х, дуги ВС=2х, дуги CD=5х, дуги DA=4х.
В сумме все эти дуги дают 360°
х+2х+5х+4х=360
12х=360
х=30.
Значит дуга АВ 30°, дуга ВС 2*30°=60°, дуга CD=5*30°=150°, дуга DA 4*30°=120°.
Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается.
Угол А опирается на дугу ВD. ВD=ВС+CD=60°+150°=210°.
∠А=210°:2=105°
Угол В опирается на дугу АС. АС=СD+DA=150°+120°=270°
∠В=270°:2=135°.
Угол С опирается на дугу DB. DB=DA+AB=120°+30°=150°
∠С=150°:2=75°.
∠D=360°-(105°+135°+75°)=45°.
ответ: ∠А=105°, ∠В=135°, ∠С=75°, ∠D=45°.
Так-с, у нас есть равнобедренный треугольник ABC. Достраиваем в нем медианы: BQ к AC и AE к BC. Этого хватит. Рассмотрим треугольник ABQ: BQ будет перпендикуляром, так как в равнобедренных треугольниках( в данном случае ABC) медиана, проведенная к основанию является так же и высотой. Следовательно, угол AQB=90 градусов. AB=10см, AQ=1/2*AC=8см, так как BQ - медиана. Теперь из прямоугольного треугольника ABQ найдем катет BQ по теореме Пифагора: BQ=корень из (AB^2-AQ^2)=корень из (10*10-8*8)=корень из (100-64)=корень из 36=6см. В равнобедренном треугольниках пересекаются в одной точке и делят друг друга на отрезки в отношении 2/1 считая от вершины. Следовательно, BO/OQ=2/1. BO=4см, OQ=2см. И теперь осталось найти AO из треугольника AOQ, где угол AQB равен 90 градусов, по теореме Пифагора: AO=корень из (OQ^2+AQ^2)= корень из (4+64)=корень из 68=4*корень из 17
Средняя линия делит боковые стороны пополам, следовательно,
АВ=АМ+ВМ, АМ=АВ:2=4÷2=2см
CD=CN+ND, ND=5:2=2,5см.
MN=(AD+BC):2=(10+15):2=7,5 см (свойство средней линии)
теперь нам известны все параметры трапеции AMND, найдём её периметр:
Р(AMND)=AM+MN+ND+AD=2+7,5+2,5+10=22см