Пусть нам известна хотя бы сторона этого шестиугольника:))). Пусть она равна а. Кстати, радиус описанной окружности тоже равен а. Этот шестиугольник состоит из 6 равных треугольников. Достаточно вычислить площадь хотя бы одного. Треугольники будут равносторонними. потому что угол при вершине треугольника, где центр этого шестиугольника, равен 360:6=60. А другие два угла равны между собой как в равнобедренном треугольнике. Значит 180-60=120 градусов - сумма двух одинаковых углов треугольника. 120:2=60 градусов - мера углов при основании треугольника. Площадь равностороннего треугольника со стороной а можно вычислить по формуле, перемножив две одинаковые стороны друг на друга, затем умножив на синус 60 градусов и разделить пополам.
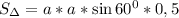
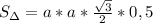
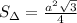
Всего таких треугольников 6. Значит надо умножить на 6.
Получается ответ
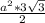
Высота ВН=6 см проведена к АD , высота ВМ=4 см проведена к DC.
ВМ ⊥ CD, но ВН не является гипотенузой прямоугольного треугольника, образованного высотами, т.к. ВМ:ВН =4/6, и это отношение не равно cos30°
ВН пересекает СD в т.К.
∆ ВКМ - прямоугольный, угол МВК=30°, след, угол ВКМ=60°. Тогда в подобном ему по общему острому углу при К прямоугольном ∆ ВКС
угол ВСК=30°
Катет ВМ противолежит углу 30°, след. гипотенуза ВС=2 ВМ=8 см.
В параллелограмме противоположные углы равны.
След. ∠ВАН=BAD=30°, и катет ВН противолежит углу 30°, ⇒ гипотенуза АВ=2 ВН=12 см.
Площадь параллелограмма равна произведению высоты на сторону, к которой проведена.
CD=AB=12 см
S= CM•CD=4•12=48 см²
* * *
Или
Площадь параллелограмма равна произведению соседних сторон на синус угла между ними:
S=a•b•sinα
S=12•6•sin30°=96•1/2=48 см