Объяснение:
Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.
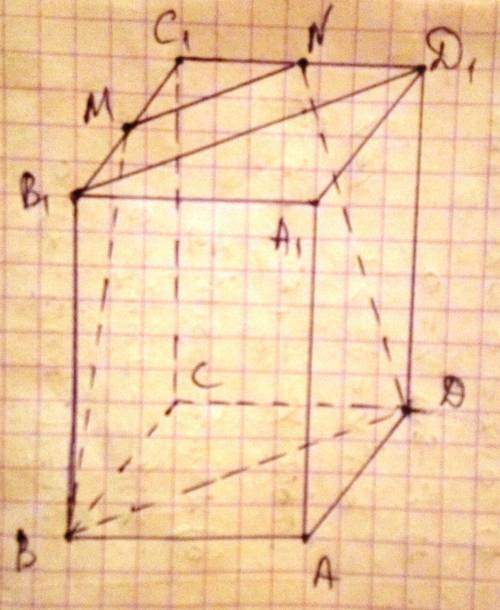
Пусть плоскость проведённая через B, D и серединную точку M ребра B₁C₁ пересекается с плоскостью B₁C₁А₁ по прямой MN. M∈B₁C₁, N∈D₁C₁.
⇒MN||BD⇒BDNM-трапеция
BD||B₁D₁; MN||BD⇒MN||B₁D₁
MN-средняя линия треугольника B₁C₁D₁
ABCDA1B1C1D1- правильный прямоугольный параллелепипед⇒ABCD-квадрат, а боковые грани прямоугольники.
B₁M=0,5B₁C₁=ND₁, DD₁=BB₁, ∠MB₁B=∠ND₁D=90°⇒ΔMB₁B=ΔND₁D⇒MB=ND⇒
⇒BDNM-равнобедренная трапеция. Ч.Т.Д.
Дано:
ABCD – равнобедренная трапеция
P(ABN)=37см
CB=7см
P(ABCD)–?
Треугольник ABN – равнобедренный (т.к.BN=CD)
В параллелограме NBCD: BC=DN=7см
В треугольнике ANB:
AB+BN+NA=AB+CD+NA=37см
AD состоит из двух отрезков: AN и ND
В трапеции ABCD: P=AB+BC+CD+DA=AB+7+CD+NA+ND=(AB+CD+NA)+7+7=37+7+7=51см
ответ: P(ABCD)=51см